Vecteurs - triangle

Bonjour, j'ai un exercice à faire où je bloque un peu, pouvez-vous m'aidez ? S'il vous plaît!
Voici l'exercice:

Soit ABC un triangle, I le milieu de [AB] , J le milieu de [AC] et k le milieu de [BC].

Soit G le point sur le segment [CI] tel que vecteur GI = 1/3 vecteur CI

Construire la figure
Prouve que vect GB + vect GA = 2 vect GI
Prouve que 2 vect GI + vect GC = vect 0
En déduire que vect GA + vect GB + vect GC = vect 0
A l’aide de la question précédente prouve que 2 vect GJ + vect GB = vect 0 et que 2 vect GK + vect GA = vect 0

6.Que peut-on en déduire quant à G ?

Merci d'avance!

Bonjour,

Piste pour démarrer,

J'espère que tu as fait la figure
Pense à la relation de Chasles

$gb⃗+ga⃗=gi⃗+ib⃗+gi⃗+ia⃗=2gi⃗+ib⃗+ia⃗\vec{gb}+\vec{ga}=\vec{gi}+\vec{ib}+\vec{gi}+\vec{ia}=2\vec{gi}+\vec{ib}+\vec{ia}$

Vu que I est le milieu de [AB] , tu as une simplification , d'où le résultat.

3) $gi⃗=13ci⃗\vec{gi}=\frac{1}{3}\vec{ci}$ donc $2gi⃗=23ci⃗2\vec{gi}=\frac{2}{3}\vec{ci}$

$gc⃗=23ic⃗\vec{gc}=\frac{2}{3}\vec{ic}$

Donc ..............

Conséquence des deux questions précédentes

C'est la figure qui me pose problème

Je ne sais pas trop où est ton problème relatif à la figure.

Peut-être pour le point G ?

Pour le point G , au début de l'énoncé , tu dois le placer sur [IC] , à 1/3 en partant de I ( ou à 2/3 en partant de C )
Dans l'exercice , on te fait démontrer que G est aussi sur [AK]
Donc on te fait démontrer que G est à l'intersection de 2 médianes [IC] et [AK] ( donc aussi sur la 3eme)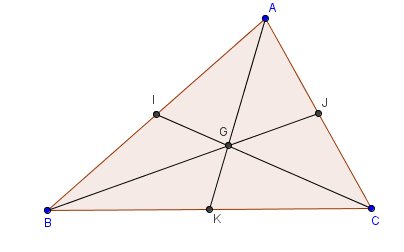

$fichier math$

J'ai pas compris là 2 et la 3 tu me la déjà faite ?

Ici , on aide mais on ne fait pas l'exercice !

Pour la 2) , relis ma réponse ( j'ai utilisé deux fois la relation de Chasles ) et termine la simplification .

Pour la 3) , tu relis aussi et tu termines.

Si tu ne comprends toujours pas , précise clairement ce qui te gène.

= vect GI
donc = vect 0
je ne sait pas

c'est $2gi⃗2\vec{gi}$
oui
Utilise les réponses précédentes:

$ga⃗+gb⃗+gc⃗=(ga⃗+gb⃗)+gc⃗=2gi⃗+gc⃗=...\vec{ga}+\vec{gb}+\vec{gc}=(\vec{ga}+\vec{gb})+\vec{gc}=2\vec{gi}+\vec{gc}=...$

2 vect IC ?

Non pour la réponse à la 4)

Tu as démontré à la question 3) que $2gi⃗+gc⃗=0⃗2\vec{gi}+\vec{gc}=\vec{0}$ donc il suffit de l'écrire.

( Pense à utiliser les résultats des questions précédentes )