Espace : intersection de droites, de plans, section, ....

On considère le cube ABCDEFGH et les points M, N et P définis par :

M milieu de [BC] vecteur CN = 2/3 (vecteur)CD EP(vecteur) = 1/4 EH(vecteur)

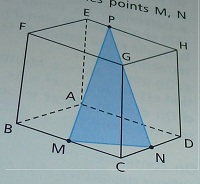
$fichier math$

Partie A (sans les coordonnées)

a. Justifier que les droites (MN) et (AD) sont sécantes en un point appelé L.

c. Déterminer l'intersection des plans (MNP) et (ADE)

d. Déterminer, et justifier la position relative, de l'intersection (d) des plans (MNP) et (EFG).

e. Les points M, N, D, H et F sont-ils coplanaires ?

f. Sur la figure ci contre, tracer la section du plan (MNP) sur le cube.

Partie B ( avec coordonnées )

On considère le repère orthonormal ( A ; AB(vecteur), AD(vecteur), AE(vecteur) ) de l'espace.

a. Donner les coordonnées des points M, N et P.

b. Déterminer une représentation paramétrique pour chacune des droites (AD) et (MN).

c. En déduire les coordonnées du point L.

d. Donner une représentation paramétrique de la droite (PL).

e. En déduire les coordonnées du point d'intersection K des droites (PL) et (DH).

f. Donner une représentation paramétrique de la droite (d).

g. Vérifier si les vecteurs HM(vecteur), HN(vecteur), DF(vecteur) sont coplanaires.

J'ai répondu à la a et à la c de la partie A
Et à la a de la B
Apres je bloque.. Merci de m'aider s'il vous plait !

BONJOUR !

*( Tu a commencé une discussion ailleurs alors , sauf nécessité , continue.) *

@loli95 Bonjour lolo , peux tu s'il te plait me dire la source de cette exercice . Merci d'avance

@Badie-Goumidi , bonjour,

@loli95 a donné cet énoncé en 2013 et on est en 2021...et comme tu peux voir, le "multi-sites" et le manque de politesse ne sont guère rentables !

Mais, pourquoi veux-tu avoir la source de cet exercice ? ? ?

Bonjour,
Vu que cet exercice a "réapparu" et qu'il n'avait pas eu de réponses il y a 7 ans (pour les raisons signalées), j'indique quelques pistes (seulement des pistes), pour consultations éventuelles.

Pistes pour la Partie A)

a) $MN→=MC→+CN→=12BC→+23CD→\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}+\dfrac{2}{3}\overrightarrow{CD}$
$MN→=12AD→+23AB→\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{AB}$
$23AB→≠0→\dfrac{2}{3}\overrightarrow{AB} \ne\overrightarrow{ 0}$ donc $MN→\overrightarrow{MN}$ et $AB→\overrightarrow{AB}$ non colinéaires.
Les droites (MN) et (AB) ne sont pas parallèles.
Elles sont coplanaires - dans le plan $(A B C D)$ -
Elles sont donc sécantes.
$(MN)∩(AD)={L}(MN)\cap (AD)=\lbrace{L \rbrace}$

c) $L$ et $P$ appartiennent aux plans $(M N P)$ et $(A D E)$ donc ces plans se coupent suivant la droite $(P L)$

Les plans $(M N P)$ et $(E F G)$ se coupent suivant la droite $(d)$ passant par $P$ et parallèle à $(M N)$

e) $H, F$ ne sont pas dans le plan $(M N D)$ qui est le plan $(A B C D)$

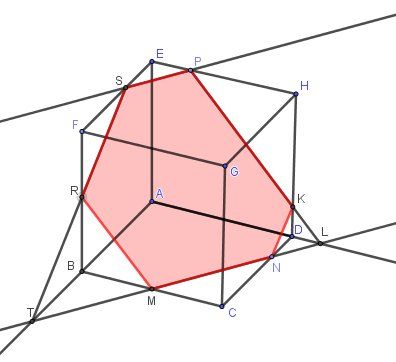
f) Section du plan $(M N P)$ avec le cube (voir la partie teintée du schéma joint (polygone MNKPSR)

Cubemodifié.jpg

Pistes pour la partie B), (calculs à effectuer)

a) $M(1,12,0)M(1,\dfrac{1}{2},0)$ ; $N(13,1,0)N(\dfrac{1}{3},1,0)$ ; $P(0,14,1)P(0,\dfrac{1}{4},1)$

b) $(A D)$ droite passant par $A$ et de vecteur directeur $AD→\overrightarrow{AD}$ .
$AD→\overrightarrow{AD}$ a pour coordonnées $(0, 1, 0)$
Soit $t_1$ le paramètre
Représentation paramétrique de $(A D$ ) :
${x=0y=t1z=0\begin{cases}x=0\cr y=t_1\cr z=0\end{cases}$

$(M N)$ droite passant par $M$ et de vecteur directeur $MN→\overrightarrow{MN}$ .
$MN→\overrightarrow{MN}$ a pour coordonnées $(−23,12,0)(-\dfrac{2}{3},\dfrac{1}{2},0)$
Soit $t_2$ le paramètre
Représentation paramétrique de $(M N$ ) :
${x=1−23t2y=12+12t2z=0\begin{cases}x=1-\dfrac{2}{3}t_2\cr y=\dfrac{1}{2}+\dfrac{1}{2}t_2\cr z=0\end{cases}$

En résolvant le système composé des représentations graphiques de $(A D)$ et $(M N)$ , on trouve

$0=1−23t20=1-\dfrac{2}{3}t_2$ <=> $t2=32t_2=\dfrac{3}{2}$
$t=12+(12)(32)=54t=\dfrac{1}{2}+(\dfrac{1}{2})(\dfrac{3}{2})=\dfrac{5}{4}$
D'où $L$ a pour coordonnées $(0,54,0)(0,\dfrac{5}{4},0)$

d) $(P L)$ droite passant par $P$ et de vecteur directeur $PL→\overrightarrow{PL}$ .
$AD→\overrightarrow{AD}$ a pour coordonnées $(0, 1, - 1)$
Soit $t_3$ le paramètre
Représentation paramétrique de $(P L$ ) :
${x=0y=14+t3z=1−t3\begin{cases}x=0\cr y=\dfrac{1}{4}+t_3\cr z=1-t_3\end{cases}$

e) $(D H)$ droite passant par $D$ et pour vecteur directeur $DH→\overrightarrow{DH}$ .
$DH→\overrightarrow{DH}$ a pour coordonnées $(0, 0, 1)$
Soit $t_4$ le paramètre
Représentation paramétrique de $(D H$ ) :
${x=0y=1z=t4\begin{cases}x=0\cr y=1\cr z=t_4\end{cases}$
En résolvant le système composé des représentations graphiques de $(P L)$ et $(D H)$ , on trouve , pour coordonnées de $K$ : $(0,1,14)(0,1,\dfrac{1}{4})$

f) (d) est la droite passant par $P$ et de vecteur directeur $MN→\overrightarrow{MN}$ .
Soit $t_4$ le paramètre
Représentation paramétrique de $(d)$ :
${x=−23t4y=14+12t4z=1\begin{cases}x=-\dfrac{2}{3}t_4\cr y=\dfrac{1}{4}+\dfrac{1}{2} t_4 \cr z=1\end{cases}$
g) les vecteurs ne sont pas colinéaires (à vérifier en calculant leurs coordonnées)

Cet exercice était un bon exercice de révision de géométrie dans l'espace.