Loi de probabilité binomiale et algorithme.
-
Bbrendouch dernière édition par
Alors voila, j'ai beaucoup de difficulté a faire cette exercice sachant ne pas répondre a plus de la moitier des question. Merci d'avance.
Une urne contient 50 boules, dont seulement 4 sot blanches. On prend successivement, au hasard et avec remise, 20 boules de l'urne. On note X la variable aléatoire Qui a pour valeurs les nombres possibles de boules blanches obtenues a la fin des 20 tirages.
Question 1 : vérifier que la valeur aléatoire X suit une loi binomiale.
Dire que c'est un schéma de Bernoulli, une épreuve de Bernoulli et une loi binomialeQuestion 2 : a) a l'aide d'une calculatrice ou d'un tableur, calculer la probabilité P(X<=5) de l'événement I : " obtenir 5 boules blanches ou moins ".
b) Définir par une phrase l’événement contraire de I.
L’événement contraire de I est : "Obtenir plus de 5 boules blanches"- a) calculer la probabilité P(X=0) de l'événement Z : " n'obtenir aucune boule blanches. "
b) justifier que l'événement contraire de Z est Z' : " obtenir au moins une boule blanche ".
C. ) en déduire la probabilité P(X>=1) de l'événement Z'.
Merci beaucoup d'avance.
-
mtschoon dernière édition par

Bonjour ( un petit "bonjour" fait plaisir ! )
algorithme ?...peut-être parles-tu de la question 2)a) ?
Vu que tu as fait environ la moitié de l'exercice , précise les résultats que tu as trouvé aux questions déja faites , et indique les questions que tu ne sais pas faire.
-
Bbrendouch dernière édition par
Bonjour , les questions que je n'arrive pas a faire sont la question 2 a), et 3 a), b) et c). Je sais que les paramètres sont n = 50 et p = 4/50
-
mtschoon dernière édition par

Tu parles d'une loi binomiale de parmètres n=50 et p=4/50 ?
Bizarre ce "n=50"...
-
Bbrendouch dernière édition par
Ba cela me semblait logique, sinon je comprend pas mon erreur désoler.
-
mtschoon dernière édition par

Relis l'énoncé :
Citation
X la variable aléatoire Qui a pour valeurs les nombres possibles de boules blanches obtenues a la fin des 20 tirages.
-
Bbrendouch dernière édition par
Donc n = 20, ba oui zut
-
mtschoon dernière édition par

et oui , n=20.
Je t'indique la formule de base ( qui doit être dans ton cours ) et qui te permets de répondre à toutes les questions.
n nombre d'épreuves(nombre de tirages) . p probabilité d'un succès ( tirer une boule blanche )
Pour k entier compris entre 0 et n :
pr(x=k)=(nk)pk(1−p)n−kpr(x=k)={{n}\choose{k}}p^k(1-p)^{n-k}pr(x=k)=(kn)pk(1−p)n−k
Ici , cela donne :
Pour k entier compris entre 0 et 20 :
$\fbox{pr(x=k)={{20}\choose{k}}\ 0.08^k \ 0.92^{20-k}}$
Je t'indique la trame de ton travail
Pour le 2)a) utiliser cette formule pour k=0 ,1,2,3,4,5 et faire la somme
Pour le 3)a) utiliser cette formule pour k=0
Pour le 3)b) faire une phrase logique
Pour le 3)c) Pr(X≥1)=1-Pr(X=0) et utiliser la réponse du 3)a)
Bons calculs.
-
Bbrendouch dernière édition par
Pour la question 2, a) comment fait on pour faire ceci sur une calculatrice ou un tableur ? C'est sur sa que j'ai des difficultés.
Et merci beaucoup pour toute ses informations.
-
mtschoon dernière édition par

Cette question dépend de tes "outils" personnels !
Si ça t'arrange , je te joins un petit programme qui fait le calcul avec Algobox, mais bien sûr , utilise les outils que tu connais !
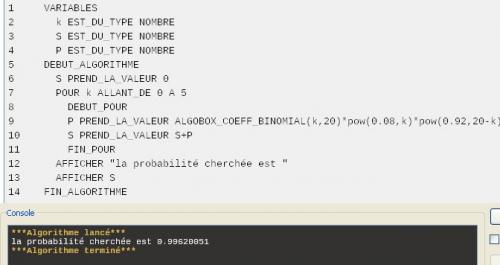
-
Bbrendouch dernière édition par
Merci bcp tout est un peu plus clair maintenant. Dernière petite question lorsque la probabilité est P(X>5) d'obtenir plus de 5 boules blanche.
Qu'est ce que l'on doit changer dans le programme ?
-
mtschoon dernière édition par

Pr(X>5)=1-Pr(X≤5) ( évènements contraires).
Tu ne changes rien au programme , tu complètes en faisant calculer 1-S