Démontrer une égalités sur angles inscrits
-
Mmathieu38150 dernière édition par Hind
Re-bonsoir, je viens de regarder l'éxercice suivant mais je ne comprend pas comment on peut demontrer que EAC=2 x ABC sachant que ce n'est pas un angle au centre.
Pour plus vous éclairer voici l'énoncer et la figure qui coïncide.Enoncé :
Les droites (BE) et (CF) se coupent en A (le point A n'est pas le centre du cercle).
Démontrer que EÂC = 2 x ABC.La figure :
Voila merci pour ce qui m'aideront .
-
Mmathieu38150 dernière édition par
La figure :
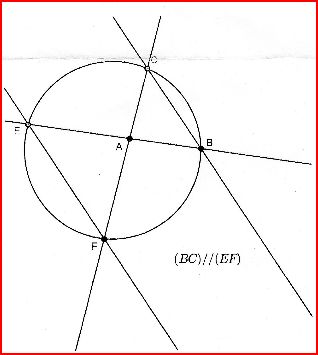
-
mtschoon dernière édition par

Bonjour,
Piste,
Il faut faire des calculs d'angles .
Avec les angles inscrits égaux , tu obtiens :
fcb^=feb^\widehat{fcb}=\widehat{feb}fcb=feb
ebc^=efc^\widehat{ebc}=\widehat{efc}ebc=efcVu que les droites sont (BC) et (EB) sont parallèles , tu as des angles alternes-internes égaux :
efc^=fcb^\widehat{efc}=\widehat{fcb}efc=fcb
ebc^=feb^\widehat{ebc}=\widehat{feb}ebc=febDe tout cela , tu peux déduire que ces quatre angles sont égaux : soit a leur valeur commune en degrés.
Après calculs , tu dois trouver eac^=2a\widehat{eac}=2aeac=2a