inconnues et relations de Pythagore

Bonjours, je viens d'entré en 1èreS et je suis déjà pomé en maths. Il y a un exercice dans mon DM que je ne comprend pas. Un peu d'aide SVP...

Sophie (la fille de monsieur x) fait la planche dans sa nouvelle piscine rectangulaire. Ses yeux se trouvent respectivement à 3,5 et 6 mètres des coins NO, NE et SE.
Déterminer à quelle distance les yeux de Sophie se trouvent du coin SO.
Faire une figure et déterminer la valeur exacte puis une valeur approchée à 1cm près de la distance recherchée.

Le professeur parle d'inconnus qui vont intervenir et de 4 relations de Pythagore.

Je ne comprend rien du tout et ne voit même pas un tout petit peu comment il faut faire... Merci à ceux qui m'aideront.

merci de donner des titres significatifs

Bonjour,

Je suppose que tu as dessiné un rectangle ( SE SO NO NE )

Tu peux appeler M , à l'intérieur de ce rectangle , le "point" où se trouve les yeux de Sophie ( évidemment , il y a deux yeux , mais ils sont proches l'un de l'autre ...)
Tu écris :
Citation
respectivement à 3,5 et 6 mètres des coins NO, NE et SE.
Es-tu sûr(e) de cette phrase , car il ya deux distances pour 3 coins ...?

Merci de vérifier.

Non justement, il n'y a que deux distances...

Je te conseille de demander une information à ton professeur et/ou tes camarades sur cette phrase ( et tu nous redemandes après si tu as besoin )

Oui, merci

J'ai le même sujet (même classe ? ^^) y a les trois valeurs, c'est 3 et 5 et 6 et non pas 3,5 et 6
Mais sinon, je trouve pas comment faire non plus..

Bonjour Robert ( ici , on dit "Bonjour" lorsqu'on arrive sur le forum )

Dedeches , si il (elle) te reconnait , pourra te remercier d'avoir compris l'écriture de l'énoncé.

Quelques pistes,

Schéma ( sans tenir compte des mesures ) :

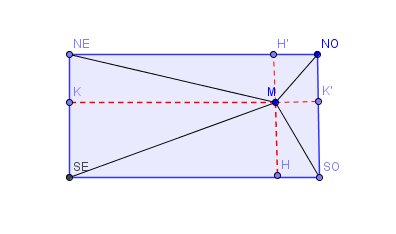
$fichier math$

On peut poser , par exemple , SE H = x , H SO= y , SO K'= z , K' NO = t

En appliquant 4 fois le théorème de Pythagore dans 4 triangles rectangles dont les hypoténuses sont respectivement M SE , M NE , M NO , M SO , on obtient :

$\left{x^2+z^2=36\x^2+t^2=25\y^2+t^2=9\y^2+z^2=m \ so\ ^2\right$

Sans chercher à trouver les valeurs des inconnues , avec les 3 premières équations, on peut trouver la valeur de y²+z² , c'est à dire de M SO ²

En prenant ensuite la racine carrée , on trouve M SO

Bons calculs .

Sinon avec les vecteurs, on prend
NO SE (en vecteur) et NE SO (en vecteur) comme on a trois mesure on trouve M SO avec les sommes des vecteurs ?

Ton idée de vecteurs me semble bien confuse car les représentants des vecteurs dont tu parles ne passent pas par le point M , donc les mesures connues ne peuvent pas être utilisées.

A toi de voir !

D'après ce qu'a écrit Dedeches : " Le professeur parle d'inconnues qui vont intervenir et de 4 relations de Pythagore ".

La piste proposée applique ce principe.