Polynôme du 2nd degré

[Pushye33]

Bonjours,

J'ai un exercice a faire pour lundi, je n'y arrive pas donc j'aimerais de l'aide, merci.

Exercice:
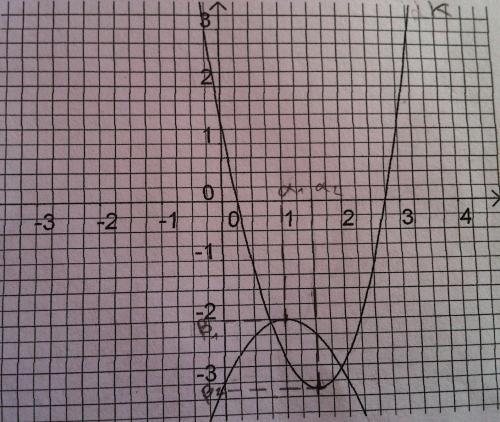
k est une fonction polynôme du second degré, avec a=2 et I est une fonction polynôme du second degré, avec a=-1.

1. Associer à chaque fonction la représentation graphique qui lui correspond.
2. Déterminer à l'aide d'une lecture graphique :
   a) la forme canonique de k et de I
   b) la forme factoriser de k. I admet-elle une forme factoriser ? Pourquoi ?
   c) les solutions de l'inéquation k(x) > 0 et I(x) > 0.

[mtschoon]

Bonjour,

Je pense que tu as bien déterminé k et I ( on voit "k" sur le schéma )

Piste pour la suite ,

Tu dois avoir des informations dans ton cours :

Pour une parabole , représentation de $p(x)=a{x}^2+bx+c$ , l'extréma étant (α,β) , la forme canonique est :

$\fbox{p(x)=a[(x-\alpha)^2+\beta]}$

Tu appliques cela à k et I :

Il faut que tu lises l'extréma de chaque parabole

Pour k , le minimum semble être le point ( 1.5 , -3)
Pour I , le minimum semble être le point ( 1, -2)

Vérifie car ton graphique n'est pas très clair et applique la formule encadrée.

[Pushye33]

Merci

[mtschoon]

De rien !

A+