Etudier la parité et la croissance d'une fonction

Bonjour/ bonsoir,

Mon problème...je dois préparer un test d'admission en math. Une des parties de ce test porte sur l'étude de fonction et là, je coule! J'ai quitté le secondaire depuis 15 ans et n'ai jamais vu ce qu'il m'est demandé. J'ai bien fait quelques recherche mais j'aurais besoin que quelqu'un m'aide pour la résolution de mes questions...donc voici...

Soit la fonction f:R → R : x→f(x)=x³-3x

a) Déterminer le domaine de fonction et l'image de la fonction f

Pour moi, le domaine c'est l'ensemble R donc D= R
Les images :
f(-3)=-18
f(-2)=-2
f(-1)= 2
f(1) =-2
f(2) = 2
f(3) = 18
Est ce exact?

b) Etudier la parité de la fonction
C'est une fonction impaire car deux abscisses opposées ont pour résultat deux ordonnées opposées à savoir f(-2)=-2 et f(2)=2

c) Déterminer les racines (zéros) de la fonction

d)Etudier la croissance de la fonction et déterminer les extrema (s'ils existent)
Une fonction croissante conserve l'ordre des images donc
a<b et f(a)<f(b)
la fonction est donc croissante sur l'interval [1;+∞[ et sur l'interval ]-∞;-1]

Une fonction décroissante inverse l'ordre des images donc
c
f(d)
la fonction est décroissante sur l'interval [-1;1]

Voilà donc mes questions et ce que j'ai pu déduire de mes recherches. C'est peut-être très simplifié...est ce correct malgré tout? Est ce possible de m'aider pour la question concernant les racines et m'orienter pour les extrema ?
Un grand merci d'avance pour votre aide précieuse!!

Bonjour,

En effet, il va y avoir du travail pour remonter la pente. Mais quand on veut on peut me disaient mes grands parents !

Le domaine de définition de la fonction f est bien IR car on sait calculer $x^3$ -3x peut être calculer pour tout x dans IR.

La question "l'image de la fonction f ", j'ai du mal à la comprendre.. Tu habites où ?

Et je le veux!
J'habite Charleroi en Belgique

Ah... Mais je crois qu'il y a un super forum de maths pour les belges qui serait plus adapté à ta situation. Je fais quelques recherches et je te dis ce que j'ai retrouvé.

Merci beaucoup!

Je suis désolée, mais ce forum fait partie de mes favoris sur mon ordinateur, or je ne suis pas chez moi. Je n'y serai pas avant lundi ... Est-ce trop tard pour ton test ?

Je présente mon test lundi en fin de journée, je vais encore faire des recherches d'ici là mais tu pourras me l'envoyer, c'est toujours utile.
Merci encore et bon week-end!

Pour continuer, pour démontrer qu'une fonction est paire ou impaire,

il faut montrer que pour tout x du domaine de définition de f, alors -x appartient aussi au domaine de définition de f et

f(-x) = f(x) alors la fonction est paire
ou
f(-x) = -f(x) alors la fonction est impaire

il faut donc montrer ici, que pour tout x dans IR, on sait que -x appartient aussi à IR, il faut donc comparer f(x) et f(-x)...

f(-x) = $x)^3$ - 3(-x)

es tu capable de démontrer si ce calcul vaut f(x) soit $x^3$ - 3x

ou f(-x) soit $x^3$ + 3x

Tu te réveilles quand même un peu tard pour rattraper ton retard !!

2 jours c'est un peu pas beaucoup....

A vrai dire, j'ai eu l'exemple du test la semaine dernière et depuis j'ai essayé de le résoudre comme je le pouvais mais sans le corrigé...
Le test porte également sur des résolutions de problèmes, d'équations et une partie statistique qui seront facile pour moi.
L'étude de fonction, ce que je réussi est un plus...

Pour la parité de fonction
par démontrer, tu veux dire calculer?
f(-2)=(-2)³-3(-2)
= -8+6
= -2
f(2)=(2)³-3(2)
= 8-6
= 2
Pour deux points d'abscisse opposés f(-2) et f(2)
j'obtiens deux ordonnées opposées 2 et -2 ce qui signifie que ma fonction est impaire

Bonjour Zorro et val797 ,

Je regarde un peu , en attendant que Zorro trouve un "super forum" en Belgique ( ce qui sera mieux car on ne sait pas ce que tu connais )

a) Oui pour les calculs des images

b) Zorro t'a expliqué pour f impaire.

Il ne suffit pas de prendre un exemple numérique pour affirmer que f est impaire sur R, l faut prouver que f(-x)=-f(x) pour tout x de R ( ensemble de définition )

$\text{f(-x)=(-x)^3-3(-x)=-x^3+3x=-(x^3-3x)=-f(x)$

La courbe représentative admet O pour centre de symétrie.

c)les "zéros" de f sont les solutions de f(x)=0

$\text{f(x)=0 \leftrightarrow x^3-3x=0 \leftrightarrow x(x^2-3)=0 \leftrightarrow x=0 ou x^2-3=0$

$\text{x^2-3=0 \leftrightarrow(x-\sqrt 3)(x+\sqrt 3)=0 \leftrightarrow{x=\sqrt 3 ou x=-\sqrt 3$

Les zéros de f sont donc 0 , √3 , -√3

Ce sont les abscisses des points d'intersection de la courbe avec l'axe des abscisses.

d) Tes résultats sont justes mais il faut les prouver.

Vu que f est impaire , pour le sens de variation , tu peux de contenter de faire l'étude pour x positif et déduire le sens de variation pour x négatif par "imparité" .

Pour 0 ≤ x ≤ 1

Soit a ≤ b , c'est à dire a-b ≤ 0

Tu peux calculer le signe de f(a)-f(b)

$\text{f(a)-f(b)=a^3-3a-(b^3-3b)=a^3-3a-b^3-3b=a^3-b^3-3(a-b)$

Il y a une identité remarquable ( si tu connais ) qui permet de factoriser :

$a^3-b^3=(a-b)(a^2+ab+b^2)$

Donc :

$\text{f(a)-f(b)=(a-b)(a^2+ab+b^2)-3(a-b)=(a-b)(a^2+ab+b^2-3)$

Sur l'intervalle [0,1] , a² ≤1 , ab ≤ 1, b² ≤ 1 donc (a²+ab+b² ) ≤ 3

donc (a²+ab+b²-3) ≤ 0

Au final :

(a-b) ≤ 0 et (a²+ab+b²-3) ≤ 0 donc (a-b)((a²+ab+b²-3) ≥ 0 donc f(a)-f(b) ≥ 0 donc

f(a) ≥ f(b) donc f décroissante sur (0,1]

Tu traites de la même façon l'intervalle [1 , +∞[ , et tu trouves f croissante.

La fonction admet donc un minimum ( relatif ) pour x=1 avec f(1)=-2 : il s'agit d'un des deux extréma .

Par imparité , tu trouves le sens de variation pour x négatif et l'autre extrema sera pour x=-1 avec f(-1)=2 ( ce sera un maximum relatif)

Bon travail !

Remarque : j'ai essayé de détailler vu l'urgence et l'importance de ton test , mais sur le forum, ,on aide les élèves à faire leur travail mais on ne fait pas le travail à leur place .
J'ai donc fait une exception !

Pour plus de clarté , je te mets le schéma ( et si tu as le droit d'utiliser une calculette graphique , je te conseille de faire d'abord la représentation graphique pour te faire une idée de ce qu'il faut démontrer ) .

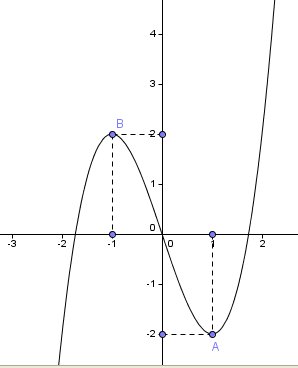
$fichier math$

Bonjour mtschoon,

Je comprends bien que c'est une exception et merci beaucoup de l'avoir faite!
En ce qui concerne le graphique, je l'ai fait et il était correct.
Pour le reste, je vais retravailler l'exercice pour mieux comprendre certains points.
Je connais la factorisation, les identités remarquables, je ne devrais pas avoir trop de mal à comprendre ce que tu m'as détaillé...
Un grand merci pour tout!

Bon courage et demande si tu as besoin d'une explication complémentaire.

Une remarque : pour le sens de variation , j'ai fait comme tu sembles connaître mais , si tu connais les "DERIVEES" , c'est plus rapide.

Les dérivées :
f(x)=x² alors f'(x)=2x
(x) =x³ alors f'(x) =3x²
(x)=ax alors f'(x) =a
etc

C'est de ça qu'il s'agit?
Si oui, peux-tu m'expliquer comment faire àpd de ça?

J'ai lu quelques choses là-dessus mais je n'ai pas trop compris
ça parlait de trouver le coefficient directeur de la tangente à la courbe de onction par une formule YB-YA/XB-XA (en admettant connaître deux pts A et B de la courbe

Si on ne connaît qu'un point A, introduire un point B:
c= (a+h)-f(a)/(a+h)-a=f(a+h)-f(a)/h

Je ne comprends pas à quoi abouti cette formule ni comment expliquer mes variations à partir de ça...

Dérivée :

$f(x)=x^3-3x$

Avec les formules usuelles :

$f'(x)=3x^2-3=3(x^2-1)$

Sur chaque intervalle où f'(x) ≥ 0 , f est croissante
Sur chaque intervalle où f'(x) ≤ 0 , f est décroissante

3 est positif , donc il te reste à étudier le signe de (x²-1)

Pour x appartenant à [0,1] : 0 ≤ x ≤ 1 donc x² ≤ 1 donc x²-1 ≤ 0 donc f'(x) ≤ 0 donc f décroissante.

Pour x appartenant à [1,+∞[ : x ≥ 1 donc x² ≥ 1 donc x²-1 ≥ 0 donc f'(x) ≥ 0 donc f croissante.

Par "imparité" , tu obtiens les cas pour x négatif.

Bonnes révisions !

Bonjour Zorro et mtschoon,

Le verdict est tombé aujourd'hui et j'ai réussi mon test d'admission en math.
Je tenais à vous remercier pour l'aide apportée!
Merci encore!

BRAVO ! ! ! ( et merci de nous avoir informé , ça fait vraiment plaisir )