Calcul d'aire et coefficient de réduction associée
-
TTitimeli 22 sept. 2013, 13:49 dernière édition par Hind 27 août 2018, 15:23
Bonjour à tous,
J'ai un exercice à faire pour demain, j'y ai passé du temps sans parvenir à faire la deuxième question.
Voici l'énoncé :
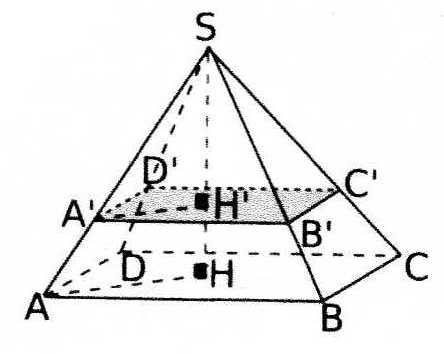
On réalise la section d'une pyramide SABCD à base rectangulaire par un plan parallèle à sa base.
AB = 12 cm
BC = 6 cm
SH = 15 cm
SH' = 10 cm- Calculer l'aire de la base de la pyramide SABCD et le volume de la pyramide SABCD.
J'ai trouvé : Base ABCD est un rectangle
Aire du rectangle = longueur x largueur
= AB x BC
= 12 x 6
= 72 cm²
Volume du rectangle = (Aire de la base x hauteur) : 3
= (72 x 15) : 3
= 1 080 : 3
= 360 cm³- Déterminer le coefficient de réduction associée à cette situation. En déduire les longueurs A'B' et B'C'.
C'est sur cette question que je bloque. J'espère que vous pourrez m'aider, merci d'avance.
Amélie
-
Bonjour Titimeli,
La hauteur passe de 15 à 10, donc un coefficient de ....
-
TTitimeli 22 sept. 2013, 15:45 dernière édition par
1,5 ?
-
De 10 à 15 c'est 1,5
mais de 15 à 10 c'est ....
-
TTitimeli 22 sept. 2013, 15:57 dernière édition par
C'est environ 0,7 alors ?
-
le coefficient est 10/15, soit 2/3.
Tu peux en déduire les longueurs A'B' et B'C'.
-
TTitimeli 22 sept. 2013, 16:20 dernière édition par
Faut-il que je fasse :
A'B' = AB : (2/3)
B'C' = BC : (2/3) ?
-
Ce n'est pas diviser mais multiplier.
-
TTitimeli 22 sept. 2013, 16:36 dernière édition par
Donc c'est :
A'B' = AB x (2/3)
A'B' = 12 x (2/3)
A'B' = 8 cmB'C' = BC x (2/3)
B'C' = 6 x (2/3)
B'C' = 4 cmMes calculs sont-ils bons ? Et comment expliquer la question du coefficient ?
-
Tes calculs sont corrects,
pour le coefficient de proportionnalité
Tu calcules le rapport
SH/SH' = 15/10 = ....
-
TTitimeli 22 sept. 2013, 19:45 dernière édition par
SH/SH' = 15/10 = 2/3
Merci beaucoup pour ton aide qui m'a été précieuse. Grâce à toi, j'ai réussi à faire mon exercice et je l'ai compris.
Je continuerai à venir sur ce site, c'est sûr !Bisous !