Fonctions et algorithmes (seconde)
-
CClaiiirette76 dernière édition par
Bonsoir !
 Je suis en seconde et mon prof de maths m'a donnée un devoir maison,mais je bloque sur une question du deuxième exercice :
Je suis en seconde et mon prof de maths m'a donnée un devoir maison,mais je bloque sur une question du deuxième exercice :
Voici deux algorithmes :
Algorithme A
Choisir un nombre
Élever au carré
Multiplier par 4
Ajouter le produit du nombre de départ par 28
Donner le résultatAlgorithme B
choisir un nombre
prendre son double
ajouter 7
prendre le carré du résultat
retrancher 49
donner le résultat- Appliquer l'algorithme A au nombre -5.
Appliquer l'algorithme B au nombre -5.
Pour un même nombre x pris au départ,les deux algorithmes aboutissent-ils au même résultat? Que peut-on dire des deux algorithmes?
. Prouver que si l'on applique l'un des algorithmes au nombre -2,on obtient le même résultat que si l'on prenait -5 au départ.
Je bloque sur celle-ci :
. existe-t-il des nombres autre que -5 et -2 qui aboutissent au même résultat après la mise en œuvre des deux algorithmes?
Merci de m'aider !
- Appliquer l'algorithme A au nombre -5.
-
Zorro dernière édition par

Bonjour
Avec un énoncé complet, on arrivera mieux à t'aider...
Dans le A
Ajouter le produit du nombre de départ par ..... à .....
Là, on ne sait pas par quoi on doit multiplier le nombre de départ et à quoi on doit l'ajouter.... C'est un peu gênant pour t'aider....
-
Zorro dernière édition par

Alors pour répondre à la question, tu prends un nombre x quelconque
Avec l'algorithme A , on a la suite de nombre :
x
x²
4x²
4x²+28xTu essayes avec le B
x
2x
2x+7
(....)² = .. ... ......etc ...
-
CClaiiirette76 dernière édition par
Donc avec B,ça fait :
x
2x
2x+7
(2x+7)² - 49
=[(2x²)+2×2x×7+7²] - 49
= (4x² + 28x+49)-49
= 4x² + 28x + 49-49
=4x²+28xOn trouve donc le même résultat. Mais après...?
-
Zorro dernière édition par

Les 2 algorithmes donnant le même résultat pour n'importe quel nombre x, que peux tu répondre à la question qui td demande s'il y a d'autres nombres que .. et .. qui marchent.
-
Zorro dernière édition par

Pas besoin de faire compliqué quand on peut faire simple...
-
Zorro dernière édition par

Donc la réponse à la question 3 est (sans faire aucun calcul)
..... Oui ou non
-
Zorro dernière édition par

Je vais supprimer les messages qui n'ont rien à faire ici...
-
CClaiiirette76 dernière édition par
Oui mais comment on fait pour trouver une autre paire de nombres autre que -5 et -2?

-
mtschoon dernière édition par

Bonjour,
Visiblement , Zorro n' a pas pu passer hier sur le forum.
Je regarde l'exercice et ta dernière question.
Si j'ai bien lu , avec l'aide de Zorro , tu as démontré qur pour tout nombre x réel , les deux algorithmes donnent le même résultat qui est 4x²+28x
J'appelle f(x) ce résultat commun :f(x)=4x2+28xf(x)=4x^2+28xf(x)=4x2+28x
Tu as calculé f(-2) et f(-5) et tu as trouvé : f(-2)=f(-5)=-40
-2 et -5 ont la même image par f
Si tu connais la représentation graphique de f : c'est une parabole ( que tu peux représenter sur ta calculette graphique , si tu sais faire )
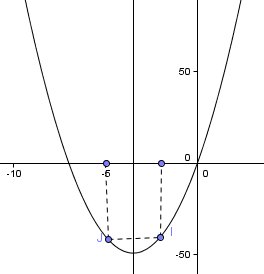
Le points I(-2,-40) et J(-5,-40) sont symétriques par rapport à l'axe de la parabole .
En utilisant cette symétrie , calcule par exemple f(-3) et f(-4) et tu dois trouver pareil :
f(-3)=f(-4)=-48
De même , f(-1)=f(-6)=-24
etc ...
Je te joins un schéma pour plus de clarté :