Calculs des coordonnées de points à l'aide des vecteurs

Je dois essayer de trouver la solution à un problème ouvert ''lieu de points'' .

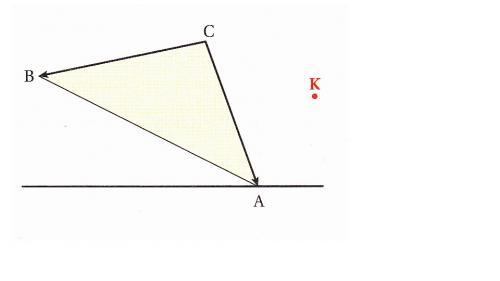
Voici l'énoncé :On considère un triangle ABC non aplati .
On définit le point K par la relation vectorielle :
AK-BK+2CK=0
Quel est le lieu des points lorsque A décrit une droite fixée ?

Je pense que ce problème est en lien avec les vecteurs ..Mais je n'arrive pas à démarrer avec le relation donnée ..Alors j'aurai besoin d'un peu d'aide ..

Bonjour,

Piste,

Transforme la relation vectorielle :

$ak⃗+kb⃗+2ck⃗=0⃗\vec{ak}+\vec{kb}+2\vec{ck}=\vec{0}$

Avec la relation de Chasles :

$ab⃗+2ck⃗=0⃗\vec{ab}+2\vec{ck}=\vec{0}$

Tu pourras déduire que : $ck⃗=−12ab⃗\vec{ck}=-\frac{1}{2}\vec{ab}$

Si tu préfères : $\fbox{\vec{ck}=\frac{1}{2}\vec{ba}}$

En appelant I le milieu de [AB] , tu auras :$\fbox{\vec{ck}=\vec{bi}} \$

Ensuite, avec un logiciel de figures dynamiques , je te sugère de "voir" où est I puis où est K, lorsque A décrit la droite (D)

Si ça peut t'aider , je te joins une figure faite avec Géogebra.
(D1) et (D2) sont les traces respectives de I et K , lorsque A décrit (D)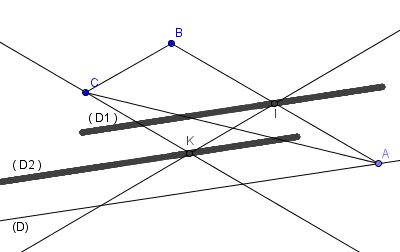

$fichier math$

Ensuite , il reste à prouver....

cette aide m'a vraiment été très utile merci beaucoup

De rien.

A+