equations - triangles rectangles

Bonjour à tous, voilà j'ai un dm a faire et il y a une question où je bloque complètement, et depuis le tout début. J'ai retourné la question dans tout les sens !

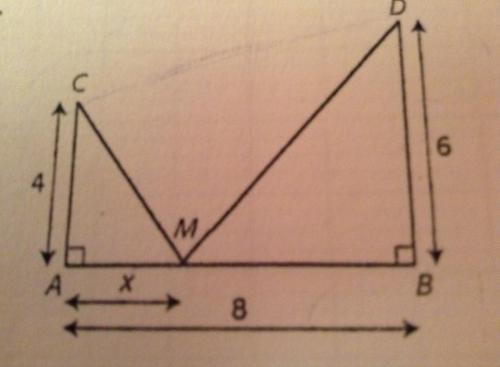
[AB] est un segment de longueur de 8cm, [AC] et [BD] sont des segments perpendiculaires à [AB] et de longueurs respectives 4 cm et 6 cm. M est un point de [AB] et x est la longueurs AM

determiner x pour que les aires des triangles AMC et BMD soient égales (fait, j'ai trouvé x = 4.8cm)
a) exprimer mc² en fonction de x (j'ai trouvé MC² = 16 + x², puis déterminer x tel que MC = 5cm (fait)

b)démontrer que MD² = x²-16x+100 (réussi)

c) déterminer x pour que les longueurs MD et MC soient égales (réussi x= 5.25cm..)

et voilà la question qui m'énerve !

d) calculer x tel que MC = 2/5 MD

Je n'y arrive pas du tout, j'ai tout essayé. Est-ce que quelqu'un peux me donner une explication svp ?

Merci beaucoup !

$fichier math$

Bonjour,

J'ai vérifié toutes tes réponses : c'est bon

Piste pour la d)

Je suppose qu'il s'agit de $\text{MC=\frac{2}{5}MD$

Par élévation au carré ( entre nombres positifs ) : $\text{MC^2=(\frac{2}{5})^2 MD^2$

$\text{MC^2=\frac{4}{25} MD^2$

En remplaçant MC² et MD² par les expressions trouvées , pour x appartenant à [0,8] , tu résous l'équation :

$x2+16=425(x2−16x+100)x^2+16=\frac{4}{25}(x^2-16x+100)$