Résoudre graphiquement une équation exponentielle avec valeur absolue

[Shizangen]

Bonjour, donc je bloque à une question, pourriez vous m'aider ? Merci

1. A l'aide de la représentation graphique de y = e^x, résoudre graphiquement |e^x-1| ≥ 0,5.

|e^x-1| = la distance est de e^x à 1, je trouve intervalle [-0,5;0,5]

[mathtous]

Bonjour,
Ta réponse est forcément fausse : 0 est dans l'intervalle [-0,5;0,5] mais |$e^0$ - 1| =0 n'est pas supérieur à 0.5

[mtschoon]

Bonjour Mathtouset Shizangen ,

• Shizangen , Mathtous t'a déjà bien aidé en te prouvant que ta réponse est inexacte.*

Un petit coup de pouce si tu n'as pas encore trouvé .

Vu l'énoncé , je te suggère de construire la courbe $C_1$ d'équation $y=e^x$

Tu déduis la construction de $C_2$ d'équation $y=e^x$-1 puis celle de $C_3$ d'équation
y=|$e^x$-1|

Tu traces la droite D d'équation y=1/2

Avec C3 et D , par lecture graphique , tu tires la conclusion demandée.

Si besoin , pour vérifier ta construction , je te joins $C_3$et D

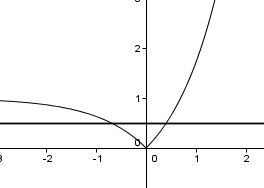
( Eventuellement , tu peux nous donner ton résultat ; nous vérifierons )

[Shizangen]

Merci beaucoup.

[mtschoon]

De rien !

Comme je te l'ai déja dit , si tu le souhaites , tu peux nous donner ta réponse ( pour vérification ) .

[Shizangen]

Bonjour j'ai tenté de construire ces 3 courbes, cependant je n'arrive pas à tracer la valeur absolue y=|ex-1| sur geogebra:

C1 : e^(x)
C2: e^(x)-1
C3: ?

[mtschoon]

Rappel :

Pour a ≥ 0 |a|=a
Pour a ≤ 0 |a|=-a

Donc :

Pour $e^x$-1 ≥ 0 : |$e^x$-1|= $e^x$-1 ( portions de courbes confondues )

Pour $e^x$-1 ≤ 0 : |$e^x$-1|=-( $e^x$-1 ) ( portions de courbes symétriques par rapport à l'axe des abscisses )

C'est ce qu'il faut que tu fasses vu que l'énoncé te demande d'utiliser $y=e^x$

Remarque : avec geogebra , la valeur absolue se note abs .
Pour C3 , c'est donc $y=abs(e^x$-1)