Demi-cercle , fonction

Bonjour, j'ai un dm à rendre et je suis bloquée sur les deux dernières questions la c) et la d), pourriez-vous m'aidez s'il vous plait? voici l'énoncé:
1.a) Résoudre dans R l'inéquation 1-x²≥0.
b) f est la fonction définie sur l'intervalle [-1;1] par: f(x)=√(1-x²)
tracer a l'écran de la calculatrice la courbe représentative de la fonction f.

c) Démontrer que dans un repère orthonormé, la courbe représentative de f est le demi-cercle de centre l'origine du repère et de rayon 1.
2.d) A partir de la définition explicite de f(x), déterminer le sens de variation de f sur [-1;1].

je vous dis merci d 'avance et j 'espère que vous pouvez m'aider!

Bonjour,
Un point de la courbe est un point M(x;y) tel que y = f(x) = √(1-x²).
Calcule y².

je ne comprend pas pourquoi il faut calculer y² et pas y tout court ?:/

Pour répondre à la question c), tu as besoin de connaître y².
Tu sais quelle forme a l'équation d'un cercle ?

x²-y²?

et pour la d)?

Chaque chose en son temps.
x² - y² n'est pas l'équation de quoi que ce soit.
L'équation d'un cercle est de la forme x² + y² + ax + by + c = 0

Je ne peux pas t'aider davantage si, à partir de y = √(1-x²), tu ne calcules pas y² comme je te l'ai demandé.

C quoi la suite

@Claire01 , bonjour,

Ici, la politesse n'est pas une option...
Y penser une autre fois.
Je te mets les consignes avant de poster:
https://forum.mathforu.com/topic/1378/stop-lire-ce-sujet-tu-devras-avant-de-poster-ton-message

@Claire01 a dit dans Demi-cercle , fonction :

C quoi la suite

J'essaie de t'indiquer la démarche.

c) Pour $x∈[−1,1]x\in[-1,1]$ , $f(x)=1−x2f(x)=\sqrt{1-x^2}$
Soit $y = f (x)$
Nécessairement $y≥0\boxed{y\ge 0}$
Par élévation au carré :
$y=1−x2y=\sqrt{1-x^2}$ <=> $y^2=1-x^2$ <=> $x^2+y^2=1$
On peut écrire $
$x-0)^2+(y-0)^2=1^2$
L'équation d'un cercle de centre I(a,b) et de rayon R est
$x-a)^2+(y-b)^2=R^2$
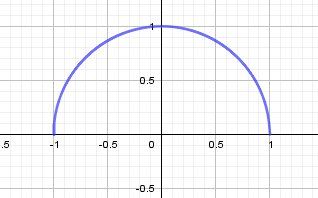
Il est donc question du cercle de centre $O (0, 0)$ et de rayon $R = 1$

Comme on a la condition $y≥0y\ge 0$ , il s'agit du demi-cercle de centre $O (0, 0)$ et de rayon $R = 1$ situé dans le demi plan au dessus de l'axes des abscisses.

@Claire01

Pour le d) bien-sûr, le sens de varaition se "vois" en regardant le demi-cercle, mais il est demandé de le trouver à partir de la définition explicite de f(x)

$f(x)=1−x2f(x)=\sqrt{1-x^2}$

Dérivée : $f′(x)=−2x21−x2=−x1−x2f'(x)=\dfrac{-2x}{2\sqrt{1-x^2}}=\dfrac{-x}{\sqrt{1-x^2}}$

$f$ est dérivable sur $] - 1, 1 [$ et son signe est le signe de $- x$

Pour $x<0x\lt 0$ , $−x>0-x\gt 0$ donc $f′(x)>0f'(x)\gt 0$ donc f strictement croissante
Pour $x>0x\gt 0$ , $−x<0-x\lt 0$ donc $f′(x)<0f'(x)\lt 0$ donc f strictement décroissante
Pour $x = 0$ , $- x = 0$ , $f^{'} (x) = 0$ f admet un maximum (qui vaut 1)

Tableau de variations , pour plus de clarté.

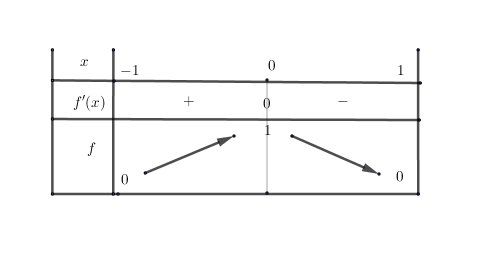
Bonne lecture.