Etudier une fonction et tracer sa courbe

Bonsoir,

Je poste ce message car j'ai un devoir maison à rendre et j'ai deux exercices dont je n'ai pas trop compris et qui je trouve sont assez complexe.
Voici l'énoncé du premier exercice :

Soit f la fonction racine carrée et g la fonction définie par g(x)=√x+1 ≥ -1

Quel est le sens de variation de g ?
a) Tracer à la main les courbes Cf et Cg représentant f et g sur [0;10]
b) Justifier la position respective de Cf et Cg
c) Qu'observe-t'on pour f(x) et g(x) pour de "grandes valeurs de x" ?

J'attends de l'aide car pour moi c'est un peu flou tous ça..

Merci d'avance.

Bonsoir,

Je suppose que tu as voulu écrire $g(x)=x+1g(x)=\sqrt{x+1}$ pour x ≥ -1

Piste pour démarrer,

La fonction x->x+1 est croissante , la fonction "racine" est croissante ; la composée de 2 fonctions croissantes est croissante donc g est ...............

Oui c'est exact.

Alors, la fonction g(x) est croissante car une racine carrée est toujours positif, ici a > 0 donc elle est croissante est-ce bien ça?

Je ne comprends pas trop "la composée de 2 fonctions croissantes".. J'ai pas tout bien suivi, pourriez-vous m'expliquer merci.

Ta première explication n'est pas bonne.

La notion de composée doit , en principe , être dans ton cours

Si besoin , tu peux , peut-être , regarder ici:

http://yallouz.arie.free.fr/premiere_cours/composee/composee.php

J'ai vérifié elle n'y est pas. Et je comprends véritablement pas trop ce cours. Nous avons pas vu ça ce terme de composée.

Enfin pour répondre à la question 1. faudrait soit dire si elle est croissante ou décroissante et puis basta?

Des explications s'il vous plaît..

Pour une explication "mathématique" , il faudrait connaître soit la composition de deux fonctions , soit la notion de dérivée .

Si tu ne connais ni l'un , ni l'autre , tu peux donner une explication toute simple (comme en seconde )

Par exemple :

Soit a et b deux réels supérieurs à -1 tels que a < b

a< b => a+1 < b+1 => $a+1<b+1\sqrt{a+1} \lt \sqrt{b+1}$ => g(a) < g(b)

Donc , la fonction g est croissante ( strictement )

D'accord. Oui en effet je n'ai pas encore vu les dérivée..

Cela est pour la question 1.
Ensuite pour la 2. a : j'ai juste à tracé deux représentation graphique ; f(x) qui est la fonction racine carré mais pour g(x) il s'agit aussi d'une fonction racine carré ou alors d'une fonction affine ?
2. b : je dois dire quand Cf est au dessous de Cg et aussi quand Cf est au dessus de Cg?

Merci

g n'est ni la fonction "racine carrée" , ni une fonction affine .

g est la composée d'une fonction affine avec la fonction "racine carrée"
( plus précisément "fonction affine suivie de la fonction racine carrée") , mais tu as dit que tu ne connaissais pas le terme , alors tu ne dis rien.

Je suppose que tu as fait les courbes pour x appartenant à [0,10] .
Tu ne dois trouver qu'un cas pour la position relative des 2 courbes ( et ensuite , tu le prouves )

a) f(x) est une fonction racine carrée croissante sur [0 ; 10]
Dans l'énoncé on me demande de tracer Cg je fais comment dan ces cas là ?
b) Je dois justifier dans le cas ou Cf est au dessus de Cg c'est ça ?
c) J'ai pas trop compris cette question.. "grande valeurs x" c'est quoi..

Merci.

Si tu ne veux pas faire de calculs à la main , utilise ta calculette graphique.
Evidement , la syntaxe n'est pas la même sur toutes les calculettes.

Idée :
Dans Y tu mets √(x+1)
Dans Windows tu mets xmin=0 , xmax=10, ymin=0 , ymax=5
Dans Graph , tu obtiens Cg
En utilisant la fonction TABLE , tu peux obtenir toutes les valeurs que tu veux pour faire la courbe

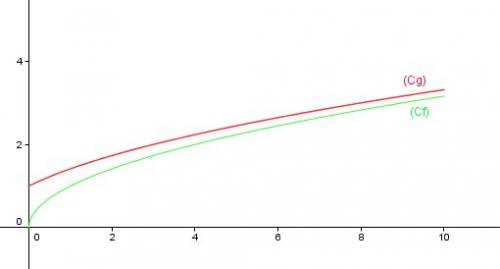
Pour te donner un aperçu , je te joins une image $fichier math$

La position de Cf par rapport Cg se voit .

Essaie de le prouver x < x+1 donc......

Merci beaucoup pour cette aide !

x < x+1 donc (Cg) est au-dessus de (Cf) sur [0 ; 10]

Pour la question 2) b. Justifier... J'ai juste à évoquer graphiquement ce que je vois c'est ça ?

Tu évoque ce que tu vois graphique et après , tu justifies .

Pour la justification , il te manque une étape :

x < x+1 donc $x<x+1\sqrt x \lt \sqrt{x+1}$ donc f(x) < g(x)

D'accord.

Et pour la dernière question?
c) Qu'observe-t'on pour f(x) et g(x) pour de "grandes valeurs de x" ?

Je ne comprends pas le terme "grandes valeurs de x". Merci de m'éclaircir un peu parce que j'ai du mal..

Lorsque tu seras plus avancé dans ton cours , tu sauras que "grandes valeurs de x" veut dire que l'on donne à x des valeurs de plus en plus grandes ( tendant vers +∞ , si tu connais )

Observe le graphique et imagine des valeurs de x plus en plus grandes , par exemple 10 , 100 , 1000,...
Que devient l'écart entre les deux courbes ? que devient la différence g(x)-f(x) ? que deviennent f(x) et g(x) ( *l'une par rapport à l'autre *) ?

En faite ce qu'on cherche, c'est l'écart entre les deux courbes si on prends un grand intervalle les deux courbes se rapproche mais se touche pas?
Faudrait peut-être que je fasse f(x)-g(x), ensuite je remplace et je calcule ?

C'est bien ça.
Les deux courbes s'approchent l'une de l'autre sans se toucher.

Tu peux effectivement faire le calcul de g(x)-f(x) pour quelques "grandes valeurs de x"
Tu peux calculer par exemple :
g(10)-f(10)
g(50)-f(50)
g(100)-f(100)
...

Cette question est une approche du cours sur les "limites"

Et ensuite je remplace x par 10/100 et le résultat que je trouve correspondra donc à l'écart entre g(x) et f(x) ?

remplacer ? ? ?

Pour une valeur de x donnée , g(x)-f(x) représente la différence des ordonnées du point de Cg d'abscisse x avec le point de Cf d'abscisse x

Par exemple :

g(10)-f(10)≈0.154

D'accord. Merci beaucoup.

J'ai une question suivant qui dit

On distingue que lors du tracé on place au même endroit sur la feuille de papier deux points distants de moins de 0,05 cm.
Pourrait-on distinguer sur legraphique de Cf et Cg d'abscisse 20? et les points d'abscisse 100? et ceux d'abscisse 200?

Pour cette question j'utilise f(x) - g(x) ?

Je trouve la phrase écrite bien confuse...
Deux points distants de moins de 0,05 cm sont placés au même endroit sur le tracé ( tellement ils sons près )

Tu calcules :

g(20)-f(20) ≈ 0.11

0.11 > 0.05 donc pour x=20 les points sont différenciés sur le tracé

g(100)-f(100) ≈0.049

0.049 < 0.05 donc pour x=100 les points sont placés au même endroit sur le tracé

Tu continues avec g(200)-f(200)

Merci énormément..

Et pour finir mon exo, j'ai une question qui dit je cite:

a) Démontré que pour tout x ≥0, g(x) - f(x) = 1 / √x+1 + √x.
b) En déduire que pour x > 0, 0 < g(x)-f(x) < 1/2√x.

Pour la question 4. a) j'avais pensé à résoudre l'équation en g(x) - f(x) en démontrant que c'est bien égale à ce qu'on a sur l'énoncé mais je ne suis pas sûr..
J'attends des réponses.

Je vous remercie.

Tout à fait ( mais il s'agit d'une égalité et non d'une équation )

$g(x)−f(x)=x+1−x=...g(x)-f(x)=\sqrt{x+1}-\sqrt x=...$

Transforme en utilisant la quantité conjuguée et tu trouveras $1x+1+x\frac{1}{\sqrt{x+1}+\sqrt x}$

Mais par quoi dois-je commencer pour résoudre cette équation? Comment fait-on pour obtenir le résultat en égalité?

Relis mon précédent message ; la méthode est indiquée.

Rappel: le conjugué de √a-√b est √a+√b

Rappel : il ne s'agit pas d'une "équation" car tu ne cherches pas la valeur de x .

J'ai relu plusieurs fois, mais je ne comprends pas votre terme quantité conjugué, ça corresponds à quoi dans l'énoncé ?

ça correspond à la question 4)a)

Je t'ai seulement donné une piste car ce serait bien que tu trouves ...

Idée :

$(a−b)(a+b)=a−b(\sqrt a-\sqrt b)(\sqrt a +\sqrt b)=a-b$ ( identité remarquable)

Donc :

$(a−b)=a−ba+b(\sqrt a-\sqrt b)=\frac{a-b}{\sqrt a +\sqrt b}$

Oui ça serait bien, mais je n'arrive pas avec vos explications.

On a g(x) = √x+1 et on a f(x) = √x
On nous demande question 4. a) de démontrer que f(x) - g(x) =

Je fais donc (√x+1) - √x, cette opération doit être égale à la quantité conjuguée mais comment pourrait là trouver ! C'est à cela que je n'arrive pas à vous comprendre.

regarde la fin de mon dernier message.

Oh mon dieu.. Mais même les identités remarquables sont mêlés à ce truc !

(√x-1 - √x) = x-1 - x / √x-1 - √x = 1 / √x-1 - √x

ça doit être bon je pense..

Presque bon , mais il y a une erreur de signe au dénominateur.

Ah oui c'est positif.

Pour la question 4. b) qui demande de déduire que pour x > 0, 0 < g(x) - f(x) < 1/ 2√x

Pour cette question, déjà il s'agit d'un encadrement. Donc que dois-je faire? J'avais pensé à déjà remplacé g(x) - f(x) par la quantité conjugué que j'ai calculé précédemment et ensuite ça se ramène à une inéquation c'est cela?

J'attends des réponses. Merci !

Oui , mais ce n'est pas une "inéquation" , c'est une inégalité .

Et comment peut-on répondre à cette question? Car je vois pas personnellement

$x+1 > x$

donc $x+1>x\sqrt{x+1} \gt \sqrt x$

donc $\sqrt{x+1}+\sqrt x > \sqrt x+\sqrt x$

donc $\sqrt{x+1}+\sqrt x > 2\sqrt x$

donc... ( je te laisse finir )

Ben ensuite, je fais passé le 2√x et j'ai une inégalité suivante :

√x+1 + √x - 2√x > 0 ?

Cela ne sert pas .

Regarde un peu ce qu'il faut prouver.

Il suffit de prendre les inverses ...tu vas y arriver .

Bonne nuit.

Au pire des cas, passez moi la réponse directement puis j'essaierais avec une explication ça serait bien, et j'essaierais de le refaire tous seul.

Merci.

a et b étant deux nombres strictement positifs :

$\gt b \rightarrow \frac{1}{a} \lt \frac{1}{b}$

Je comprends vraiment rien, excusez-moi mais c'est cela qui faut dire.

Vous mélangez les a et les b, avec des divisés, ainsi que des x.. Vous m'excuserez mais j'ai du mal un peu à vous suivre.

Répondez à la question, et m'expliquez comment vous trouvez ça puis moi-même j'essaierais de comprendre avec vos explications et votre réponse c'est à dire comment du pourquoi avez vous trouvez cela.

Merci encore..

Dur , dur...

Je te donne eu exemple :

$\gt 2 \rightarrow \frac{1}{3} \lt \frac{1}{2}$

Dans une division dans $r^*_+$ , plue le diviseur est grand , plus le quotient est petit

Donc , pour répondre à ta dernière question ,

Tu sais que : $\sqrt{x+1}+\sqrt x > 2\sqrt x$

Tu intilises la propriété $\gt b \rightarrow \frac{1}{a} \lt \frac{1}{b}$ en remplacant a par $x+1+x\sqrt{x+1}+\sqrt x$ et b par $2x2\sqrt x$ et tu trouveras l'inégalité souhaitée.