Position relative entre deux courbes
-
Nninetyfivee dernière édition par
Bonjour,
On considère les deux fonction f et g définie par f(x)= 1/(x-3) et g(x)= x-3
Représenter graphiquement sur la calculatrice les deux fonctions et en déduire une conjecture relative entre leurs courbes représentativesPouvez-vous m'aider svp, je n'ai jamais vu ça en cours.
-
Mmathtous dernière édition par
Bonjour,
D'abord, précise le domaine de f.
Ensuite, tu peux chercher les coordonnées des points d'intersection des deux courbes.
-
Nninetyfivee dernière édition par
Le domaine de f, c'est l'ensemble de défnition ? Car on me pose la question avant et j'ai mis que c'était R mais je ne suis pas sûr.
-
Mmathtous dernière édition par
Il s'agit bien de l'ensemble de définition, mais celui de f n'est pas R : il y a un quotient qui ne doit pas être nul.
-
Nninetyfivee dernière édition par
Et comment es-que je dois faire pour trouver car je suis habituée a avoir une équation du second degres?
-
Mmathtous dernière édition par
Si tu sais résoudre une équation du second degré, tu sais forcément résoudre une équation du premier degré, comme en quatrième.
Le dénominateur de f(x) est x-3.
Il ne doit pas être nul.
Mais pour quelle valeur de x, x-3 est-il nul ?
-
Nninetyfivee dernière édition par
Pour 3 ?
-
Mmathtous dernière édition par
Oui, donc il faut exclure 3.
Le domaine de f est R{3}.
-
Nninetyfivee dernière édition par
D'accord, merci. Mais je ne sais toujours pas comment répondre à ma question..
-
Mmathtous dernière édition par
Citation
Ensuite, tu peux chercher les coordonnées des points d'intersection des deux courbes.Pour cela, tu dois résoudre l'équation 1/(x-3) = x-3, étant entendu que x doit être différent de 3.
La voilà ton équation du second degré.
-
Nninetyfivee dernière édition par
je trouve cette équation du second degrès :
-x²-x-3=0 C'est ca ?
-
Mmathtous dernière édition par
Non.
Tu multiplies des deux côtés par (x-3) :
1 = (x-3)²
Ne développe surtout pas :
(x-3)² - 1 = 0
Factorise.
-
Nninetyfivee dernière édition par
Je trouve alors :
x²+6x-10
-
Mmathtous dernière édition par
C'est faux, et je t'avais conseillé de factoriser et pas de développer.
-
Nninetyfivee dernière édition par
Je n'arrive pas à trouver ..
-
Mmathtous dernière édition par
Sais-tu factoriser a² - b² ?
Ici, il faut factoriser (x-3)² - 1 = (x-3)² - 1²
-
Nninetyfivee dernière édition par
Je ne comprends pas.. Ca fait 0
-
Mmathtous dernière édition par
Non:
a² - b² = ??
-
Nninetyfivee dernière édition par
bah ca fait x²-9
-
mtschoon dernière édition par

Bonjour Mathtous et ninetyfivee ,
Je ne fais que passer !
Je me permets une parenthèse ...si ça peut aider .
Vu la question posée "conjecturer" , je joins un graphique
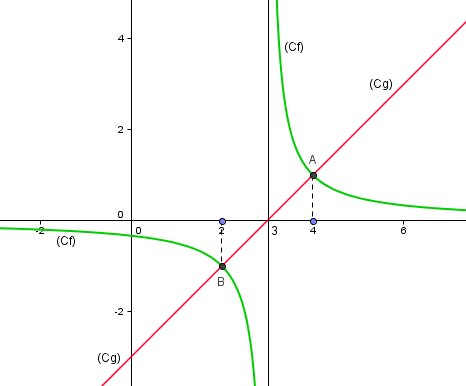
ninetyfivee , avec le graphique , tu peux conjecturer ( seulement "conjecturer" ) ,suivant x , la position relative des deux courbes
Pour x=4 ( point A ) et pour x=2 ( point B ) : Cf coupe Cg
Cela correspond aux propositions de Mathtous , pour lesquelles tu n'as pas terminé le calcul .
Pour x < 2 et pour 3 < x < 4 : Cf au dessus de Cg
Pour 2 < x < 3 pour x > 4 : ...............................( tu complètes )
-
Mmathtous dernière édition par
Non, ça ne fait pas x²-9.
Oui ou non, connais-tu l'identité a² - b² = ???Regarde le graphique fourni par Mtschoon (et que tu dois avoir sur ta calculette) : tu peux y lire les abscisses de A et B : cela a un lien direct avec ce que je t'ai demandé : résoudre (x-3)² - 1 = 0