droites parallèles (vecteurs)

Soit A b et C trois points non alignés
Soit D et E les points tels que : BD(vecteur)=4/3BB(vecteur) et DE(v)=-1/4AD(v)

Le but de l'exercice est de démontrer que la droite (AB) est parallèle à la droite (CE)

1.PLacer les points D et E sur la figure et émettre une conjecture sur la position des droites (AB) et (CE)

2.Premiere méthode : calcul vectoriel
a)exprimer le vecteur AB en fonction des vecteurs BC et AD
b)exprimer le vecteur CE en fonction des vecteurs BC et AD
c)en déduire que les droites (AB) et (CE) sont parallèles

3.Deuxième méthode : avec des coordonnées

on se place dans un le repère (B ; BC; BA)
a)Déterminer les coordonnées des points A,B et C
b)Calculer les coordonnées des points D et E dans ce repère
c)Calculer les coordonnées des vecteurs BA et CE
d)Conclure

Je n'y arrive pas du tout j'ai relue mon cour mais même avec ca je ne sais pas ce comment faire merci pour votre aide

BONJOUR quand même !

Citation
Soit D et E les points tels que : BD(vecteur)=4/3BB(vecteur) et DE(v)=-1/4AD(v)

revois ce que tu as envoyé car pour moi BB(vecteur) signifie :

$bb⃗=0⃗\vec {bb}=\vec {0}$

Bonjour Zorro et satsuki,

satsuki , un petit "Bonjour" fait plaisir...

Une prochaine fois , relis ton message avant de poster...

Je suppose que tu as voulu écrire $bd⃗=43bc⃗\vec{bd}=\frac{4}{3}\vec{bc}$

Si c'est bien cela , voici un schéma pour t'aider à démarrer :

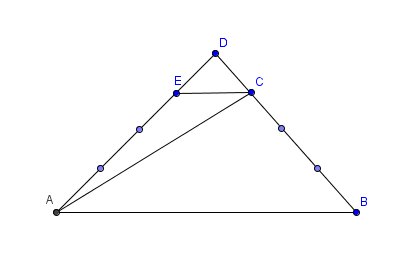
$fichier math$

Tiens nous au courant.