Problèmes dans les vecteurs
-
Ccoshy95 dernière édition par
Léa fabrique un mobile ci-contre :
La masse de la tige est négligeable. La lune L a pour masse mlm_{l}ml et le soleil S a pour masse msm_{s}ms. Ces deux masses sont non nulles.
Léa veut savoir en quel point, noté G, accrocher le fil pour que son mobile reste en équilibre.
D'après la loi d'Archimède, il y a équilibre lorsque :ms×gs=ml×glm_{s}\times gs = m_{l}\times glms×gs=ml×gl
Voici le schéma :
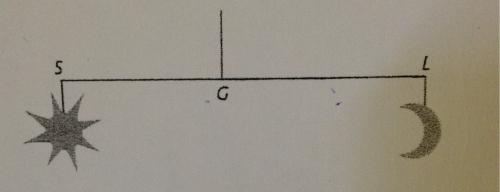
Et voici les questions :
-
Que peut-on dire des directions et des sens des vecteurs gs⃗\vec {gs}gs et gl⃗\vec {gl}gl ?
-
En déduire que msgs⃗+mlgl⃗=0⃗m_{s}\vec {gs}+m_{l}\vec {gl}=\vec {0}msgs+mlgl=0
-
En utilisant la formule de la question 2), montrer que sg⃗=−ml−ms−mlsl⃗\vec {sg}=\frac{-m_{l}}{-m_{s}-m_{l}}\vec {sl}sg=−ms−ml−mlsl
-
a) Si ml=msm_{l}=m_{s}ml=ms, où est situé le point G ?
b) Si ms=30gm_{s}= 30gms=30g et ml=10gm_{l}= 10gml=10g, où est situé le point G ?
Je n'ai pratiquement rien compris à ce qu'il fallait faire, pourriez-vous me donner des pistes ? Svp
-
-
mtschoon dernière édition par

Bonsoir,
Piste pour démarrer,
-
Les vecteurs gs⃗\vec {gs}gs et gl⃗\vec{gl}gl sont colinéaires ( de même direction ) et de sens contraire.
-
Vu que , en plus , msgs=mlglm_s gs=m_lglmsgs=mlgl
Tu peux déduire que :
msgs⃗=−mlgl⃗m_s \vec{gs}=-m_l\vec{gl}msgs=−mlgl
En transposant , tu trouves l'égalité voulue.
- Urtlise la relation de Chasles , appliquée à l'égalité du 2)
-
-
Ccoshy95 dernière édition par
Ok merci pour les deux premiers,
mais pour le trois je dois décomposer sl⃗\vec {sl}sl avec la relation de Chasles ou bien sg⃗\vec {sg}sg ?
-
Ccoshy95 dernière édition par
Et sur la formue du 2) : le "-" il agit sur mlm_{l}ml et gl⃗\vec {gl}gl, ou que sur mlm_{l}ml ?
-
mtschoon dernière édition par

Je te réponds dans l'ordre des questions de l'énoncé.
Pour la 2)
−mlgl⃗- m_l\vec{gl}−mlgl est l'opposé de mlgl⃗m_l\vec{gl}mlgl
Pour plus de clarté , tu peux écrire :−(mlgl⃗)- (m_l\vec{gl})−(mlgl)
Remarque :
−(mlgl⃗)=+(−ml)gl⃗)=+ml(−gl⃗)=+ml(lg⃗)- (m_l\vec{gl})=+(- m_l)\vec{gl})=+ m_l(-\vec{gl})=+ m_l(\vec{lg})−(mlgl)=+(−ml)gl)=+ml(−gl)=+ml(lg)
Cela n'est pas utile ici ( c'est seulement une remarque )
Pour la 3)
C'est gl⃗\vec{gl}gl qu'il faut décomposer en gs⃗+sl⃗\vec{gs}+\vec{sl}gs+sl