Fonction pour trouver l'aire minimale d'un triangle

Bonjour,

Est-ce que vous pourriez m'expliquez un peu (et assez clairement si possible) ce que c'est qu'une aire minimale d'un triangle ? J'ai cherché partout mais je n'arrive toujours pas à comprendre... Comment faire pour avoir un aire minimale ?
Voici mon exercice pour que vous compreniez :

"On considère un carré ABCD de côté 10cm.
Sur le côté [AB] on place un point L .
on pose AL = x (en cm) et onn place sur [DA] un point P tel que DP= xcm.
On construit alors le triangle LCP.

Le but est de déterminer s'il existe un triangle LCP d'aire minimale et si oui lequel.
on appelle f la fonction qui à tout x de [0 ; 10] associe l'aire du triangle LCP. "

J'avais déjà trouvé une personne qui avait aussi posé cette question mais la réponse qu'elle avait eu était " l'aire de CPL = aire du carré - les aires des triangles autour " ce que j'ai fait, mais j'ai eu x= 5 et A(CPL) = 39.13 ce qui n'est pas assez minimale ...

J'espère avoir était clair et merci pour l'aide !

Bonjour,

Tu n'as pas tout trouvé sur ce sujet .

Avec Google , je viens de trouver au moins 4 sites qui ont traité cet exercice.

Je viens de faire les calculs.

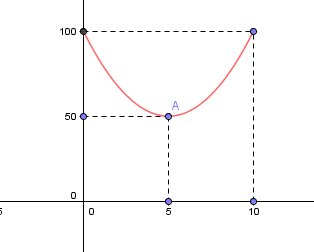
Tu dois trouver aire(LCP)=f(x)=2x²-20x+100 pour 0 ≤ x ≤ 10

f est une fonction du second degré.

Le minimum est bien pourx=5maisce minimum est f(5)=50

Je te joins la représentation graphique

$fichier math$

Donne nous tes calculs si tu as besoin, et nous vérifierons.