Montrer que deux événements A et B barre sont indépendants
-
Ddodo16 dernière édition par Hind
Bonjour
Énoncé:
On considere E un univers et A,B deux evenements de E qui sont indépendantsMontrer que A et B barre sont indépendant
Merci
-
mtschoon dernière édition par

Bonjour,
Je suppose que tu sais que
a‾∩b‾=aub‾\overline a \cap \overline b=\overline {a u b}a∩b=aub
(Sinon , il faut le prouver )
Piste,
p(a‾∩b‾)=p(aub‾)=1−p(aub)p(\overline a \cap \overline b)=p(\overline {a u b})=1-p(a u b)p(a∩b)=p(aub)=1−p(aub)
p(a‾∩b‾)=1−[p(a)+p(b)−p((a∩b)]p(\overline a \cap \overline b)=1-[p(a)+p(b)-p((a \cap b)]p(a∩b)=1−[p(a)+p(b)−p((a∩b)]
p(a‾∩b‾)=1−p(a)−p(b)+p(a∩b)p(\overline a \cap \overline b)=1-p(a)-p(b)+p(a \cap b)p(a∩b)=1−p(a)−p(b)+p(a∩b)
Tu remplacesp(a∩b)p(a \cap b)p(a∩b) par p(a)×p(b)p(a)\times p(b)p(a)×p(b)
En factorisant , tu dois arriver à (1−p(a))×(1−p(b))(1-p(a))\times (1-p(b))(1−p(a))×(1−p(b)) c'est à dire à p(a‾)×p(b‾)p(\overline a)\times p(\overline b)p(a)×p(b)
Bon calcul.
-
Ddodo16 dernière édition par
Pardon je m'en suis mal exprimer il n'y a que B qui sous la forme B barre
-
mtschoon dernière édition par

Donc, reprenons...............
a=(a∩b)∪(a∩b‾)a=(a \cap b) \cup (a\cap \overline b)a=(a∩b)∪(a∩b)
a∩ba \cap ba∩b et a∩b‾a \cap \overline ba∩b sont disjoints
Donc
p(a)=p(a∩b)+p(a∩b‾)p(a)=p(a \cap b) +p (a\cap \overline b)p(a)=p(a∩b)+p(a∩b)
Donc en transposant :
p(a∩b‾)=p(a)−p(a∩b)=p(a)−p(a)×p(b)p (a\cap \overline b)=p(a)-p(a \cap b)=p(a)-p(a)\times p(b)p(a∩b)=p(a)−p(a∩b)=p(a)−p(a)×p(b)
Tu mets p(A) en facteur et au final , tu trouveras p(a)×p(b‾)p(a)\times p(\overline b)p(a)×p(b)
-
Jewel HADDAD dernière édition par
@mtschoon Bonjour, je n'ai pas compris comment vous aviez trouvé : que
a barre ∩ b barre= a barre U b barre (ligne 1 de votre calcul)et puis comment est ce que :
1 - p(a) - p(b) + p(a) x p(b)
= ( 1- p(a) ) x ( 1 - p(b) )y a t-il une regle que je ne connais pas?
-
mtschoon dernière édition par

@Jewel-HADDAD , bonjour,
Pour la première ligne du calcul, il s'agit d'une loi de Morgan que tu peux facilement réaliser avec un schéma.
Je te mets un lien :
https://www.bibmath.net/dico/index.php?action=affiche&quoi=./m/morgan.htmlPour ta seconde qustion, il s'agit d'une factorisation :
1−p(a)−p(b)+p(a)p(b)=(1−p(a))−p(b)(1−p(a))1-p(a)-p(b)+p(a)p(b)=\biggr(1-p(a)\biggr)-p(b)\biggr(1-p(a)\biggr)1−p(a)−p(b)+p(a)p(b)=(1−p(a))−p(b)(1−p(a))
En mettant (1−p(a))(1-p(a))(1−p(a)) en facteur, on trouve :
1−p(a)−p(b)+p(a)p(b)=(1−p(a)(1−p(b)1-p(a)-p(b)+p(a)p(b)=(1-p(a)(1-p(b)1−p(a)−p(b)+p(a)p(b)=(1−p(a)(1−p(b)
-
Jewel HADDAD dernière édition par
Merci beacoup pour votre aide, je voulais aussi savoir si deux evenements sont independants et on souhaite calculer l'union entre ces deux evenements pouvons nous simplement faire:
1 - P (intersection de ces deux evenements)
au lieu de faire
P(A) + P(B) - P (A inter B)
-
Jewel HADDAD dernière édition par
-
Jewel HADDAD dernière édition par
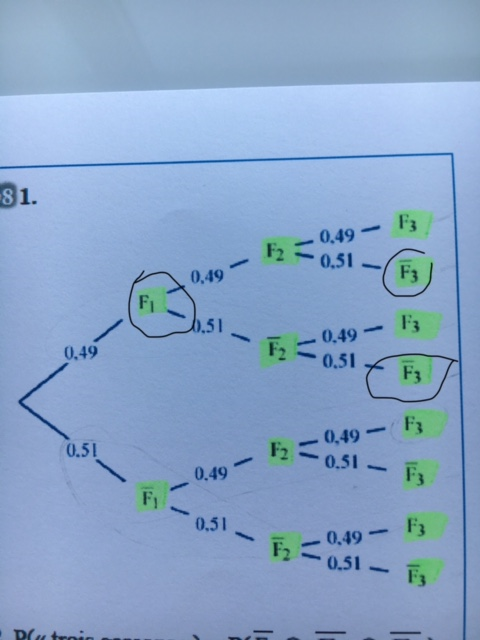
voici l'arbre et je cherce l'union des evenements F1 et F3barre
-
Jewel HADDAD dernière édition par
Du coup, moi j'ai fait:
P (F3barre Union F1 ) = P (F3barre ) + P (F1) - P(F3barre intersection F1) = 0,51 + 0,49 - 0,2499 = 0,7501
-
Jewel HADDAD dernière édition par
Mais vu que P (F3barre ) + P (F1) = 1 , j'aurais juste peux mettre 1 a la place, est ce que c'est le cas pour toutes les proba indepednantes?
-
mtschoon dernière édition par mtschoon

Bonjour,
Je trouve ce que tu dis est confus en ce qui concerne A et B indépendants.
Peut-être parles-tu de l'union.De façon générale p(A∪B)=p(A)+p(B)−p(A∩B)p(A\cup B)=p(A)+p(B)-p(A\cap B)p(A∪B)=p(A)+p(B)−p(A∩B)
Pour A et B indépendants , p(A∩B)=p(A)p(B)p(A\cap B)=p(A) p(B)p(A∩B)=p(A)p(B)
Donc, pour A et B indépendants : p(A∪B)=p(A)+p(B)−p(A)p(B)p(A\cup B)=p(A)+p(B)-p(A)p(B)p(A∪B)=p(A)+p(B)−p(A)p(B)Dans l'arbre donné, F1,F2,F3F_1,F_2,F_3F1,F2,F3 sont indépendants.
Cet arbre est un cas très particulier où l'arbre "ressemble" à un arbre de Bernouilli (avec exclusivement des probabilités de 0,49 et 0,51 à tous les niveaux de l'arbre).
Ainsi, ce que tu dis est exact dans ce cas particulier.A ta dernière question que tu poses , je répondrais : non.
-
Jewel HADDAD dernière édition par
Merci beaucoup pour votre aide.
Donc si j'ai bien compris, c'est juste pour cet arbre que P (F3barre ) + P (F1) = 1 et que P (F3barre Union F1 ) = P (F3barre ) + P (F1) - P(F3barre intersection F1) = 0,51 + 0,49 - 0,2499 = 0,7501
-
mtschoon dernière édition par

Oui, dans ce cas particulier.