vecteurs et parabole.

Bonjour,
Je dois rentre un devoir maison pour le Lundi 06 Janvier mais je suis bloqué a certains exercices.
J'ai réussi a faire le A et le D mais je ne comprends pas les autres.
Je vous fais parvenir une image de ce devoir maison :

En espérant que vous puissiez m'aider,
Merci.

Bonjour,

S'il te plait , écrit l'énoncé à la main , scanne l'image seule et mets la .

A :
Visualisation avec geogebra (Si vous faites un zoom il faut conserver le repère orthornormal).
Avec géogebra :
-Saisir f(x) = x^2
-Créer un curseur nommé a allant de -3 a +3 avec un incrément de 0.05
-Créer un point A=(a,f(a))
-Créer la droite Di=Droite[(a,0),A]
-Créer la tangente T de la parabole en A : T = Tangente[A,f]
-Puis Ds = symétrique[Di,t] la symétrie de Di par rapport à T
-Animer A et éventuellement afficher la trace de Ds
-Que constatez vous?

B :
Angles et symétries
On a le dessin ci-contre d'après le fichier géogebra. Dans ce dessin, u est un vecteur directeur de T et u'un vecteur directeur de Ds.
Justifier (par la symétrie et la relation de Chasles que :
(i;u') = π/2 + 2(i;u) [2π]

C :
Angle et coefficient directeur
On rappelle que tan(x) = sin(x) / cos(x)

Justifier que le coefficient directeur d'une droite est la tangente de l'angle orienté formé par un vecteur directeur de l'axe des abscisses et un vecteur directeur de la droite.
En déduire que tan((i;u)) = 2a où a est l'abscisse de A.

D :
Un peut de trigonométrie
Démontrer que :
tan((π/2)-x) = 1 / tan(x)
tan((π/2)+x) = -(1/tan(x))
tan(2x) = (2tan(x)) / 1- (tanx(x))²
(Utiliser les formules : sin(2x) = 2sin(x)cos(x) et cos(2x) = cos(x)²-sin(x)²).

E :
Retour sur Ds
Déduire de tout ce qui précède que : tan(i;u') = -(1-4a²)/4a)
En conclure que une équation de la droite Ds est : y-a² = -((1-4a²)/(4a)) ×(x-a)
Vérifier alors que ce que vous avez constaté au A. est vrai.

F :
Application
Si la parabole est un miroir et que Di est un rayon lumineux, que permet de conclure le résultat précédent d'après les lois de la réflexion en optique?
Où est-ce utilisé dans la "vraie vie"?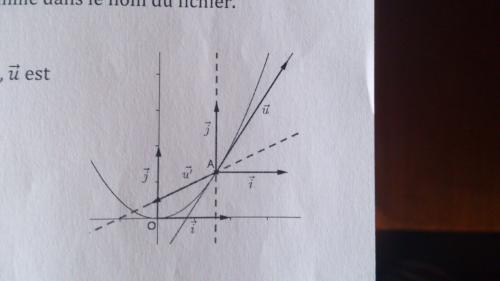
Merci encore!

Bonjour ( et bonne année 2014 ! )

Piste pour la B)

Trace le vecteur $\text{-\vec{u}'$ , opposé de $\text{\vec{u'}$ et aussi vecteur directeur de (Ds)

Par symétrie , tu peux écrire :

$\text{(-\vec{u'},\vec{u})=(\vec{u},\vec{j})$

Ensuite , tu décomposes ces vecteurs avec la relation de Chasles :

$\text{(-\vec{u'},\vec{i})+(\vec{i},\vec{u})= (\vec{u},\vec{i})+(\vec{i},\vec{j})$

$\text{(-\vec{u'},\vec{i})+(\vec{i},\vec{u})=(\vec{u},\vec{i})+\frac{\pi}{2}$

$\text{\pi-(\vec{i},\vec{u'})+(\vec{i},\vec{u})=(\vec{u},\vec{i})+\frac{\pi}{2}$

Tu transposes , tu réduis et tu dois trouver la relation souhaitée.

Merci pour ta réponse et bonne année!
J'ai fait ce que tu m'as dit pour π-(i,u')+(i,u) = (u,i) + π/2
Mais à la fin je trouve π + (i,u) = π/2 + 2(i,u)
C'est presque le bon résultat mais juste que j'ai le π eu facteur Dr gauche sur je n'arrive pas à enlever...

Je ne sait pas trop ce que tu as fait car il n'y a pas de u' dans ton expression.

$\text{\pi-(\vec{i},\vec{u'})+(\vec{i},\vec{u})=(\vec{u},\vec{i})+\frac{\pi}{2}$

Tu transposes :

$\text{-(\vec{i},\vec{u'})=(\vec{u},\vec{i})+\frac{\pi}{2}-(\vec{i},\vec{u}) -\pi$

$\text{-(\vec{i},\vec{u'})=-(\vec{i},\vec{u})+\frac{\pi}{2}-(\vec{i},\vec{u}) -\pi$

$\text{-(\vec{i},\vec{u'})=-(\vec{i},\vec{u})-\frac{\pi}{2}-(\vec{i},\vec{u})$
Tu regroupes et tu multiplies chaque membre par -1 : tu dois obtenir l'égalité voulue.

Ah d'accord, merci beaucoup!!
Pour le C, je ne comprends vraiment pas la 1ere question...

Piste , mais je ne sais pas ce que tu connais exactement sur les tangentes, alors adapte...

Soit α une mesure de l'angle $\text{(\vec{i},\vec{ab})$

Soit (AB) une droite ( non parallèle à l'axe des ordonnées )

Pour $x_A$ ≠ $x_B$ , son coefficient directeur a est :

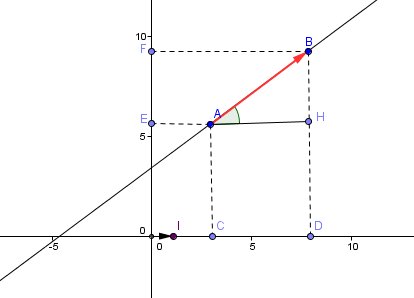
$a=yb−yaxb−xa=ef‾cd‾=hb‾ah‾=tanαa=\frac{y_b-y_a}{x_b-x_a}=\frac{\overline{ef}}{\overline{cd}}=\frac{\overline{hb}}{\overline{ah}}=tan \alpha$

$fichier math$

Ok merci!
Juste je ne comprends pas comment tu passe de : yb-ya / xb-xa = EF/CD

$y_b=y_f \ y_a=y_e \ x_b=x_d \ x_a=x_c$

Ah d'accord merci beaucoup!

Comment prouver que tan(i,u) = 2a?
C'est la question 2 du C.

Tu dois savoir que le nombre dérivé est le coefficient directeur de la tangente .

f(x)=x² donc f'(x)=2x donc f'(a)=...

Ah mais oui.... Je suis vraiment débile des fois
Par contre pour le E, je trouve que tan(i,u') = 4a / 1-4a² en utilisant la 3eme formule du D. Comment trouver le bon résultat?

Que dire...

Il y a plusieurs formules à utiliser.
Recomptes tes calculs.
peut-être as-tu fait une erreur en prenant l'inverse ?

Je viens de compter ; le résultat donné par l'énoncé est bien le bon.

Si tu as besoin, donne nous tes calculs et nous vérifierons.

Moi j'ai juste remplacer tan(x) par 2a donc du coup j'ai pas 2tan(x) / 1-(tan(x))² mais 4a / 1-4a².
J'utilise la mauvaise formule peut etre?

$\text{(\vec{i},\vec{u'})=\frac{\pi}{2}+2(\vec{i},\vec{u})$

$tan(i⃗,u′⃗)=tan(π2+2(i⃗,u⃗))\text tan(\vec{i},\vec{u'})=tan(\frac{\pi}{2}+2(\vec{i},\vec{u}))$

Tu utilises la seconde formule du D , et tu continues

Oui je l'avais déjà faites cette formule mais a la fin je trouve : Cos(2(i;u)) / sin(2(i;u)) Je ne vois vraiment pas ou je me trompe.

$tan(i⃗,u′⃗)=tan(π2+2(i⃗,u⃗))\text tan(\vec{i},\vec{u'})=tan(\frac{\pi}{2}+2(\vec{i},\vec{u}))$

Avec la seconde formule du D , tu obtiens :

$\text tan(\vec{i},\vec{u'})=-\frac{1}{tan(2(\vec{i},\vec{u}))$

Ensuite , tu utilises la 3eme formule du D

Ah oui merci!

Je comprends vraiment pas l'autre question avec y-a² = - 1-4a² / 4a (x-a)

Tu peut dire que l'équation est de la forme y=mx+p

Elle a pour coefficient directeur m= -(1-4a²)/4a)

d'où : y= -(1-4a²)/4a)x+p

Cette droite passe par A (a,a²): cela te permettra de trouver p

Ensuite , en transformant un peu , tu trouveras l'équation proposée.

Si on transforme on trouve que p = y - mx c'est bien ca?
Si c'est ça, on trouve bien que p = -3a² + a?

je ne pense pas...

p=a²+(1-4a²)/(4)

tu le gardes ainsi pour trouver l'expression voulue

Donc on a y = (-(1-4a²) / (4a))x +a² + (1-4a²) / (4a)
Donc y-a² = (-(1-4a²) / (4a))x + (1-4a²) / (4a), mais apres on fait quoi?
J'imagine qu'il faut calculer - 1-4a² / 4a (x-a) mais quand je développe je trouve pas la même chose qu'en haut.

dur dur...

y-a² =
**(-)(1-4a²) / (4a)**x +
(1-4a²) / (4)

Regarde ce qui est en rouge et fait attention au signe .

Je vois vraiment pas la....

y-a² =
-((1-4a²)/(4a))(x-a)

Pourquoi (x-a) moi j'ai trouvé (x-1)

Bon tant pis, merci quand même pour ton aide précieuse!
Je n'hésiterai pas à revenir pour un autre éxo.
Merci et à bientot!

Tu as écrit (x-1) au lieu de (x-a) car tu as confondu (1-4a²) / (4a)x avec (1-4a²) / (4)
Le dénominateur n'est pas le même.

J'espère que tu as trouvé.

Bon DM.