Donner la nature du quadrilatère

J'ai un exercice de math assez difficile qu'il faut que je fasse, mais je n'y comprend absolument rien du tout! veuillez m'aider s'il vous plait!

Voici l'énoncé :

Soit un parallélogramme ABCD de centre O
Soit I,J,K et L les symétriques respectifs de A,B,C et D par rapport à B,C,D et A

démontrer que les vecteurs : BI = KD. En déduire que O est le milieu de [IK]
Démontrer de même que O est le milieu de [IK]
En déduire la nature du quadrilatère IJKL

$fichier math$

Bonjour,
Attention, I est défini de deux manières contradictoires. Ne serait-ce pas O le centre de ABCD ?
Commence par faire une figure, joins-la (regarde en bleu sous les messages : "Ajoute une image").

Ah excusez moi voilà j'ai modifié mon énoncé ! C'était une faute de frappe. Je vais joindre la figure.

OK.
Tu y verras déjà plus clair.

J'y ai inséré la figure que j'ai faite, je pense que les points sont placés comme dans l'énoncé (qui n'y indique aucune figure)

Ta figure est fausse : tu y places les points I,J,K,L confondus avec D,A,B,C.
Or cela ne correspond pas à l'énoncé. Ainsi I est le symétrique de A par rapport à B signifie que B est le milieu de [AI].
Peut-être l'adjectif "respectifs" t'a-t-il gêné ?
I est le symétrique de A par rapport à B
J est le symétrique de B par rapport à C
K est le symétrique de C par rapport à D
L est le symétrique de D par rapport à A.

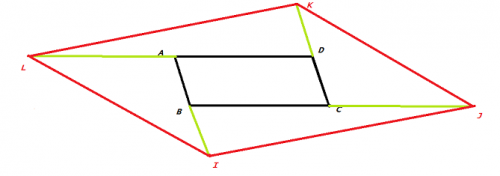
voici la nouvelle figure :

$fichier math$

les lignes vertes sont juste les traits de constructions (que je fais en pointillé sur ma feuille)

(vous pouvez constater mes lacunes en mathématiques!!) la figure est faite "à main levé" par ordinateur

Cette fois c'est juste.
Traduis par des égalités de vecteurs le fait que ABCD est un parallélogramme.
Traduis de même le fait que I est le symétrique de A par rapport à B, et que K est le symétrique de C par rapport à D.
Tu vas en déduire une nouvelle égalité de vecteurs.

Alors, voici l'égalité de vecteurs démontrant que ABCD est un parallélogramme :

→ → →
AB + BC = AC

Je ne suis pas sûre de ça :

Voici les égalités traduisant que I est le symétrique de A par rapport à B :

→ →
IB = IA

et que K est le symétrique de C par rapport à D :

→ →
KD = KC

(les flèches ne sont pas correctement placés au dessus des points IA et KC)

Sans mettre de flèches : il sera sous-entendu qu'il s'agit de vecteurs :

AB+BC = AC : c'est la relation de Chasles, elle est vraie dans tous les cas, même si ABCD n'est pas un parallélogramme. Cette égalité ne traduit donc pas l'énoncé.

IB = IA : non, regarde ton dessin, il doit t'aider. Tu vois bien que IA a une longueur plus grande que IB.
En outre, puisqu'il s'agit de vecteurs, l'égalité IB = IA impliquerait que A et B sont confondus, ce qui n'est pas le cas en général.
Même remarque pour KD = KC

Ah, par exemple pour les points ABI, je sais que I est la symétrique de A par rapport à B, c'est à dire que B est le milieu de [AI]

L'égalité est donc : AB = BI et je dois en faire de même pour démontrer l'autre égalité ?

Oui, mais il faut également traduire le fait que ABCD est un parallélogramme par une égalité vectorielle.

ABCD est un parallélogramme donc :

AB = DC

Les vecteurs, oui.
Tu as donc :
AB = DC
AB = BI
Il en manque une (avec K).

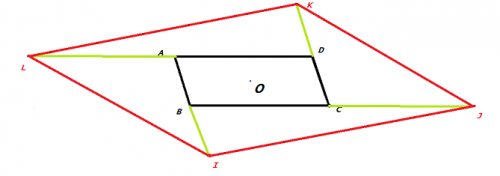
$fichier math$

Je viens de rajouter le point O.

AB = DC
AB = BI
et enfin KD = DC

Est-ce juste ?

Oui, conséquence ?

Le fait que AB = DC, vue que AB = BI alors BI = DC
et je sais que KD = DC également, alors BI = KD aussi, ?

Évidemment.
BI = KD (les vecteurs) : qu'est-ce que cela traduit ?

Excusez-moi, je n'ai pas compris le sens de "traduire", c'est-à-dire ???

Je vais quand même tenter de vous répondre : cela traduit le fait qu'elles sont de même sens, de même longeur et de même direction ?

Bien sûr ("ils", les vecteurs, pas "elles"), mais cela ne fait pas avancer l'exercice.
Quand je t'ai demandé de "traduire" le fait que ABCD est un parallélogramme par une égalité de vecteurs, tu as fourni l'égalité AB = DC.
Mais tu dois savoir que la réciproque est vraie (attention : avec des vecteurs, pas avec de simples longueurs).
Si AB = DC alors ABCD est un parallélogramme.
Ici, tu as BI = KD, alors ?

J'ai quelques difficultés à ce niveau !
Je vais sûrement dire une énorme bêtise, mais

Si BI = KD alors BIDK est un parallélogramme ?

Dire des bêtises est indispensable pour progresser.
Malheureusement ici, tu n'as dit aucune bêtise. Ce que tu as écrit est parfaitement correct : BIDK est un parallélogramme.
Avant de continuer, essaie d'expliquer ce qui te gêne : la notion de vecteur ?

En math je ne suis pas douer pour cette logique des vecteurs, notamment que -je mentionne les mots de mon professeur de mathématique - c'est un exercice assez difficile car on vient juste d'entamer le chapitre. Donc c'est plutôt certains termes ou la formulation des questions qui m'embrouillent, justement avec l'exemple du mot "traduire" je ne savais pas son sens ! Sinon on va dire que c'est un thème avec lequel globalement j'ai quelques lacunes, mais voilà après je ne sais pas vous dire exactement ce qui me gêne mais j'essaye le plus possible de m'améliorer en notant des notions non acquises !

Par contre, pour répondre à la première partie de la question une donc je re-mentionne ce dont on vient de dire, mais le fait que BIDK est un parallélogramme va me permettre de démontrer quelque chose d'autre ?

J'utilise peut-être un vocabulaire suranné (je suis très vieux).
Pour moi, "traduire" signifiait ici "écrire sous une autre forme équivalente".
Par exemple ABCD est un parallélogramme peut se "traduire" par vectAB = vectDC (mais aussi par AD = BC), les deux propriétés étant équivalentes :

Si ABCD est un parallélogramme, alors AB = DC (les vecteurs).
Et réciproquement :

Si AB = DC (les vecteurs), alors ABCD est un parallélogramme (en admettant les parallélogrammes "aplatis").
En seconde, la notion de vecteur est fortement liée à celle de parallélogramme. Il faut donc avoir toujours présent à l'esprit la propriété rappelée ci-dessus. Ensuite, c'est une question d'habitude. Il est donc normal d'éprouver quelques difficultés au début.

Citation
le fait que BIDK est un parallélogramme va me permettre de démontrer quelque chose d'autre ?Évidemment, regarde la question posée (en déduire que ...) et souviens-toi des propriétés élémentaires des parallélogrammes.

Merci de vos conseils et exemples, cela m'aide beaucoup !!

Faut-il utiliser la propriété des diagonales ?

Oui.

(Je cite sa propriété Si un quadrilatère est un parallélogramme, alors le point d'intersection des diagonales est son centre de symétrie. Or, ici j'ai O, centre de ABCD, et je sais que BIDK est un parallélogramme et que AB = BI et que KD = DC, alors le point O est le milieu du segment [IK] ?

Hmm... le raisonnement est douteux.
Le centre (centre de symétrie en fait) d'un parallélogramme est le milieu commun de ses diagonales (les diagonales d'un parallélogramme ont le même milieu).
ABCD est un parallélogramme, donc son centre O est le milieu du segment [BD] (aussi de [AC] mais cela ne sert pas pour le moment).
BIDK est un parallélogramme, donc ses diagonales ont le même milieu. Mais ses diagonales sont justement [BD], et aussi [IK].
Donc le milieu de [IK] est le même que celui de [BD] : O.

Comme tu peux le constater, ici seule la propriété des diagonales intervient, pas les vecteurs. D'où ma remarque du début : n'utilise que ce qui est nécessaire sinon tu risques de t'embrouiller et de donner un raisonnement incomplet ou faux.

Ah je viens de comprendre ! C'est à dire qu'il fallait dire que BD c'était la diagonale du parallélogramme ABCD et aussi de BIDK, c'est à dire que O est le centre de BD dans le parallélogramme ABCD donc il l'est également pour le parallélogramme BIDK ? Donc cela fait que IK qui est la seconde diagonale du parallélogramme BIDK a obligatoirement pour centre O ?

Oui, "milieu", pas "centre" (bien que le milieu d'un segment soit aussi son centre de symétrie).

D'accord!

Pour la question numéro 2, il faut que je la démontre par une "équation" ?

Citation
Démontrer de même que O est le milieu de [IK]Il y a une erreur d'énoncé : on vient juste de démontrer que O est le milieu de [IK].
Il s'agit à coup sûr de "Démontrer de même que O est le milieu de [JL]".

"De même", cela signifie par une méthode tout à fait analogue à la précédente.
Il suffit donc de reprendre entièrement la question 1 en changeant certaines lettres.
Toutefois, ne fait pas cela de façon "automatique" : ce serait sans intérêt.
Revois ce qu'on a fait, et essaie de le refaire pour [JL], sans regarder ce qui précède.

Il n'y a pas ici d'équation (au sens habituel) à résoudre.

Mon professeur s'est sûrement trompé, mais je vais le faire on ne sait jamais !
Je vais essayer de le faire sans regarder !

Je vais d'abord commencer par démontrer que LA = CJ

Je sais que ABCD est un parallélogramme, alors AD = BC, je sais aussi que L est la symétrique de D par rapport à A, alors A est le milieu de [LD], donc je sais alors aussi que LA = AD, de même pour J, la symétrique de B par rapport à C, donc C est le milieu de [BJ], et donc BC = CJ.

Je sais donc que :

AD = BC
LA = AD
BC = CJ

Je sais que AD = BC, et étant donné que LA = AD, alors LA = BC également, et alors je sais que CJ = BC, donc CJ = LA aussi.

L'égalité CJ = LA me permet d'en déduire que LACJ est un parallélogramme.

Je vais pouvoir démontrer que O est le milieu de [JL].

Je sais que [AC] est la diagonale du parallélogramme ABCD, et elle est de milieu O, je sais également que c'est la diagonale du parallélogramme LACJ qu'elle donc également pour milieu O, donc la deuxième diagonale [LJ] de LACJ aura obligatoirement O pour milieu.

Est-ce juste?

(Et ma rédaction fait-elle brouillon?)

C'est très bien !
Tu sembles avoir compris le raisonnement.
Attention toutefois à l'ordre des lettres : le parallélogramme est LAJC (et pas LACJ), dont les diagonales sont bien [LJ] et [AC].
Quant à la rédaction, Ne dis pas que [AC] est "la" diagonale : c'est "une" diagonale du parallélogramme (il y a deux diagonales).
Évite les tirets devant les vecteurs : on peut les prendre pour des signes indiquant l'opposé.
Quand tu rédigeras "au propre", n'oublie pas les flèches sur les vecteurs, sinon il s'agirait de longueurs et le raisonnement deviendrait alors faux.
Ceci dit, ta rédaction est claire.
Quant à l'erreur d'énoncé, elle est évidente (c'est bien sans doute une faute de frappe) : il suffit de lire la question suivante pour en être convaincu.

C'est noté, je corrigerai tout cela !

Pour la toute dernière question, la numéro 3, il me suffit juste de dire la nature ou de démontrer également ?

Il faut démontrer, bien sûr ("en déduire ...").

Je sais que O est le milieu des segments [IK] et de [LJ], cela me suffit-il pour prouver que c'est un parallélogramme ?