Devoir maison vecteurs : seconde

Bonjour, j'ai un exercice de DM où j'ai quelques difficultés :

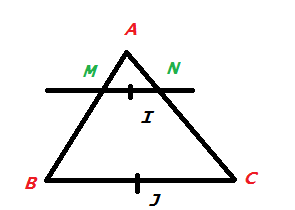
Soit un triangle ABC.
Soit les points M et N tels que (vect)AM = 1/3 (vect)AB et (vect)AN = 1/3 (vect)AC

Soit I le milieu du segment [MN] et J le milieu du segment [BC]
Que peut-on dire des points A,I et J ? Démontrer votre proposition.

Bonjour,
Si vectAM = 1/3.vectAB, alors vectMA = 1/3. ?

Alors vectMA = 1/3.vect.BA ?

Oui.
Maintenant, utilise la relation de Chasles pour décomposer vectMN.

Serait-ce :

(en prenant en compte les flèches au dessus des vecteurs)

Etant donné que I = 1/2 MN alors MI = IN

?

Citation
I = 1/2 MNNon : I est un point alors que 1/2.MN est un vecteur.
C'est MI = IN = 1/2.MN qui traduit le fait que I est le milieu de [MN].
Tu vas avoir besoin de ce résultat, mais ce n'est pas la question que je t'avais posée : la relation de Chasles est un outil indispensable à la manipulation des vecteurs:
MN = MA + ??

D'accord !

Alors : MN = MA + NA ?

Ou bien plutôt MN = MA + AN *

Non, non.
La relation de Chasles est dans ton cours. Elle traduit la façon d'ajouter deux vecteurs.
MN = MA+AN : le même point (ici A) doit terminer le premier vecteur et commencer le second.
Tu dois être capable d'écrire de telles égalités avec des points quelconques, dans le noir, la tête en bas.
Par exemple, indique-moi les égalités justes et celles qui sont fausses dans la liste suivante :

AB + BA = AC
MO + OP = MP
MO + OP = PM
AI + IJ = AJ
BC + AB = AC

PS : je n'avais pas vu ton autre message : pour éviter que des messages se croisent, évite d'en envoyer plusieurs à la suite : attends une réponse.
Tu peux aussi modifier un message comme je viens de le faire ici, mais cela peut ne pas être vu tout de suite.

(Ah d'accord désolée!)

; 3) ; 5) sont fausses
; 4) sont justes ??

Il y avait un petit piège pour la 5 : l'addition des vecteurs est commutative : on peut l'effectuer dans n'importe quel ordre, comme pour des nombres usuels :
3 + 7 = 7 + 3.
De même, BC + AB = AB + BC (j'ai changé l'ordre des termes, mais je n'ai pas modifié les vecteurs, bien sûr).
Et maintenant je peux appliquer la relation de Chasles :
BC + AB = AB + BC = AC

Donc je devais faire ainsi pour répondre à la question précédente ? (MN = MA + ??)

Tu as répondu, après correction :
MN = MA + AN
Maintenant, remplace MA et AN en fonction de ce que donne l'énoncé :
MA = 1/3.BA (ce que je t'avais demandé au début) et AN = 1/3.AC

MN = 1/3.BA + 1/3.AC ?

Oui, mais tu sais que k.u + k.v = k.(u+v) où u et v sont des vecteurs et k un nombre réel.
Donc, tu peux mettre 1/3 en facteur.

C'est à dire 1/3.(BA+AC) ?

Oui, et que vaut BA + AC ?

BA + AC = BC ?

Oui. Résumons : MN = 1/3.BC
Tu as fait une figure ? Tu peux voir qu'effectivement (MN) et (BC) sont parallèles, que les vecteurs MN et BC sont de même sens, et que MN est 3 fois plus petit que BC (il s'agit en fait d'une traduction vectorielle du théorème de Thalès).

Maintenant, on s'intéresse aux points I et J.
On a déjà vu que MI = IN = 1/2.MN (les vecteurs).
Fais de même pour J.

Voici la figure "à main levée" par ordinateur :

$fichier math$

BA + AC = BC

et BJ = JC = 1/2.BC ?

(puis-je en déduire que BC = 3.MN ?)

Oui.
MN = 1/3.BC, MI = 1/2.MN, BJ = 1/2.BC, il en résulte que MI = k.BJ
Que vaut k ?

MI = 1/3.BJ ?

Exact, ça se lit sur le dessin, mais sais-tu conduire les calculs qui amènent à ce résultat ?

Il faut que je parte de quelles valeurs ?

Puisque tu cherches une égalité sur MI, tu peux partir de MI = 1/2.MN, puis remplacer MN ...

(c'est une partie compliquée pour moi)

MI = 1/2.MN et BJ = 1/2.BC

mais je ne sais pas par quoi continuer? (je n'ai aucun exercice de colinéarité comme celle-ci sur mon cahier, on a pas appris à calculer comme ça pour l'instant donc c'est difficile)

Je ne vois pas d'autre possibilité que d'utiliser la colinéarité des vecteurs puisqu'on te demande de démontrer que les points A,I,J sont alignés (on le voit sur la figure).
MI = 1/2.MN et MN = 1/3.BC, donc MI = (1/2).(1/3).BC = 1/6.BC
Mais BJ = 1/2.BC, donc BC = 2.BJ
Je remplace dans l'égalité précédente : MI = 1/6.BC = (1/6).2.BJ = 1/3.BJ

Je résume :
MI = 1/3.BJ, et on sait que AM = 1/3.AB
Alors on peut exprimer AI à l'aide de la relation de Chasles :
AI = ...

(je voulais dire par là que le thème de la colinéarité est en cours d'apprentissage dans ma classe)

donc AI= 1/3.AJ ?

Détaille :
AI = AM + MI (relation de Chasles)
AI = 1/3.AB + 1/3.BJ (résultats établis)
AI = 1/3.(AB + BJ) (propriété de la multiplication des vecteurs par un nombre)
AI = 1/3.AJ (relation de Chasles)
Qu'est-ce que cela prouve ?

Cela doit prouver alors que AI et AJ sont colinéaires et A est un point commun. Donc les points AIJ sont alignés ?

C'est ça.

Merci de m'avoir aidé!
Mais j'aimerai m'entraîner encore sur ce genre d'exercices, vous ne connaîtrez pas par hasard un site permettant de nous entraîner sur les vecteurs ?

Je ne connais pas de sites particuliers sur ce sujet.
Mais en tapant "vecteurs" dans la rubrique "chercher" (en haut de la page grise), et en précisant le niveau "seconde", tu dois pouvoir trouver d'autres exercices ici.

Merci beaucoup!

De rien.
Bon courage.