Déterminer graphiquement les solutions d'une équation

Bonjour,

Je fais mon DM et le dernier exercice me pose problème ! J'ai trouvé quelques réponses mais je ne pense pas qu'elles soient justes... Voici l'énoncé :

John souhaite décorer la pièce principale d'un grand tableau de 4 mètres sur 3. Le peintre chargé de sa réalisation pense que, pour être harmonieux, ce tableau devra respecter la condition suivante : l'air du contour (en blanc) devra être égale à l'aire de la partie peinte (en gris).
On désigne par x la largeur du contour (en mètre).
La condition proposée par le peintre est réalisée si et seulement si 2x^2-7x + 3 = 0
On considère f la fonction définie pour tout nombre réel x par : f(x) = 2x^2 -7x + 3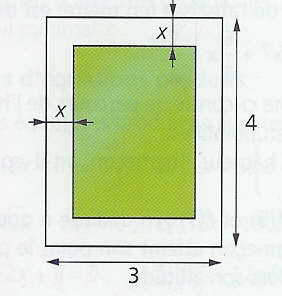

$fichier math$

Représenter f(x) dans un repère : 1cm = 1m (Déjà fait)
Déterminer graphiquement les solutions de l'équation f(x)= 0 MA REPONSE : pour x= 0,5 et pour x= 3
Quelle largeur x de la bande le peintre devra-t-il choisir ? Je ne sais pas si c'est 0,5 ou la seconde : 3
Démontrer que, pour tout nombre x appartenant à l'intervalle [0;3], f(x) = (x-3)(2x-1) Je ne sais pas comment faire...
Retrouver le résultat de la question 3.

Quelqu'un peut m'aider s'il vous plaît ?

Bonjour,
On ne te demande pas de démontrer la condition 2x² - 7x + 3 = 0 ?
Question 3 : la largeur du tableau est 3m. Peut-on alors choisir x = 3 ?
Question 4 : puisqu'on te donne la réponse, tu peux te contenter de vérifier, en développant (x-3)(2x-1), que tu retombes bien sur 2x² - 7x + 3

Si, mais j'y ai déjà répondu...
En ce qui concerne la question 3, en effet je pense également qu'on peut choisir x=3...je pense que c'est la meilleur solution mais bon on n'est jamais sur de rien !

Pour la question 4, je retombe bien sur 2x²-7x+3 mais je ne sais pas quoi faire avec l'intervalle ? Est-ce que je dois prendre une valeur de l'intervalle pour le démontrer ?

Citation
je pense également qu'on peut choisir x=3Mais non : il ne resterait plus de place pour la peinture.

Citation
mais je ne sais pas quoi faire avec l'intervalle ? Est-ce que je dois prendre une valeur de l'intervalle pour le démontrer ?Surtout pas : tu ne démontrerais rien du tout avec une valeur particulière.
Avoir développé prouve que l'égalité est vraie pour toutes les valeurs de x, donc en particulier si x ∈ [0;3]

Donc pour la question 3 : Je choisie la valeur x = 0,5 en justifiant que si on prenais la solution x=3 il ne resterait plus de place pour la peinture ?

Oui, refais un dessin en prenant x = 1,4. Tu verras qu'il reste encore de la place pour la peinture verte, mais pas beaucoup.
En réalité, l'énoncé est mal posé. x peut varier entre 0 et 1,5 ces valeurs devant d'ailleurs être exclues si on veut pouvoir peindre (x < 1,5) et avoir quand même une bordure blanche (x > 0).
Donc en fait, x ∈ ]0;1,5[
Cette fois, 3 est en dehors, et la seule valeur acceptable est 0,5.

Mais dans la question 5, il me dise de justifier la question 3, donc pour justifier je fais un calcul ou bien je fais le même résonnement que vous ?

Non ils disent de retrouver le résultat de la question 3 pardon, pcq la 3 a été faite graphiquement donc je suppose qu'à la 5 je dois faire un calcul ?
Si à la 3 j'ai repondu x= 0,5
Probablement qu'à la 5 je dois utiliser f(x) = (x-3)(2x-1) pour retrouver le résultat à la 3 ?

Je pense plutôt qu'il s'agit de retrouver les résultats de la question 2.
Le raisonnement que j'ai fait précédemment, c'est pour répondre à la question 3, pas pour la "retrouver".
Tu as résolu graphiquement l'équation f(x) = 0, maintenant, grâce à la forme factorisée, tu vas pouvoir la résoudre algébriquement.

Sur mon dm il y a écrit retrouver le resultat de la question 3...je trouve ça bizarre...
Mais je pense que je vais faire ce que vous avez dit : la résoudre algébriquement
x-3 = 0 ou 2x-1= 0
x= 3 2x= 1
x= 1/2

Je retrouve bien les réponses de la question 2...et celle que j'ai choisi à la 3

Parfait.

Merci beaucoup !

De rien.
Bon courage.