Derivées de fonctions

Bonjours a tous, j'ai un problème avec ce devoir maison, je ne vois pas du tout comment faire, j'ai essayer de calculer les équations de droites des tangentes et leurs coefficients directeurs mais rien a faire... Un peu d'aide serait la bienvenue ! Merci d'avance a ceux qui éclairciront mes heures de travail qui n'aboutissent a rien !

Bonjour,

$fichier math$

Merci d'écrire tes questions à la main.

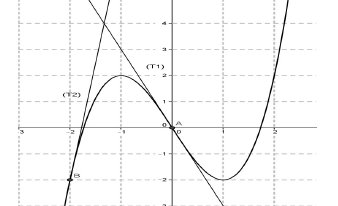
On donne ici la représentation graphique d'une fonction f et deux de ses tangentes. T1 est la tangente a Cf au point A(0;0) et T2 sa tangente au point B(-2;-2).

Déterminer en justifiant vos réponses :
1.a) f'(-2) b) f'(0)
2. Déterminer graphiquement les solutions de l’équation f'(x)=0

Bonjour,
La dérivée d'une fonction en un point (nombre dérivé) est le coefficient directeur de la tangente à la courbe en ce point.
Pour f'(0), on arrive à lire le graphique : f'(0) semble valoir -3.
Mais pour l'autre tangente, le dessin est insuffisamment précis : n'est-il pas plus haut (on verrait alors sur quel point du quadrillage passe (T2).
Approximativement, il semblerait que f'(-2) vaille 8. Mais impossible d'être précis faute d'un graphique suffisant.

Je ne peux pas donner les réponses comme ça, il me faut les justifier avec des calculs...
De ce fait tout sera précis. Mais je n'arrive pas a trouver les calculs a faire...

J'ai réussi pour f'(0) mais pour f'(-2) je n'y arrive pas. Le prof en cours nous a dit qu'il fallait utiliser les coordonnées du point d'intersections des deux tangentes, mais je ne voit pas comment faire.
J'ai trouvé l’équation de droite de T1 qui est y= -3x

C'est juste pour (T1).
Pour le point d'intersection des deux tangentes, l'ordonnée semble être 4. Mais pour l'abscisse, c'est peu précis : il semble qu'elle vaille -4/3.
Si tu supposes que c'est juste, tu peux alors trouver l'équation de (T2) et donc f'(-2).

Bonjour mathtous,

Cela me semble tout à fait exact le -4/3 que tu suggères

Pour le point d'intersection des deux tangentes, l'ordonnée semble être 4

L'équation de (T1) est y=-3x

$\leftrightarrow x=-\frac{4}{3}$

Bonjour Mtschoon,
En effet, si on admet y = 4, on peut "calculer" x.
C'est comme pour (T1) : on est bien obligé d'admettre qu'elle passe par le point (-1;3).

Les "lectures graphiques" sont à la mode...

Je n'aime pas trop. Pour moi le graphique sert à déceler des erreurs "visibles", ou à conjecturer, mais je n'apprécie guère qu'il fournisse des données.

Pour la question 2. Je n'y arrive pas ... vous pourriez m'aider ?

Mathtous t'expliquera mieux lorsqu'il passera pas là

En attendant, comme il n'est pas là, je te donne une piste.

Tu sais que le nombre dérivé f'(x) est le coefficient directeur de la tangente à la courbe au point d'abscisse x.

Les valeurs de x telles que f'(x)=0 sont donc les abscisses des points de la courbe pour lesquels le coefficient directeur de la tangente est nul.

Une droite dont le coefficient directeur est nul est une droite parallèle à l'axe des abscisses

donc......................

J'ai compris mais je ne trouve quand meme pas la réponse...

Regarde bien la courbe et les deux points où les tangentes ( non véritablement tracées, mais facilement imaginables ) sont parallèles à l'axe des abscisses.

( Par exemple, imagine la tangente à la courbe au point d'abscisse 1 )