Problème avec des aires et des fonctions
-
KKN dernière édition par
Bonjour j'aimerais avoir de l'aide pour ce problème :
Un morceau de bois a une forme de prisme droit dont la base est un
triangle isocèle.
Un menuisier doit découper une poutre parallélépipède de volume
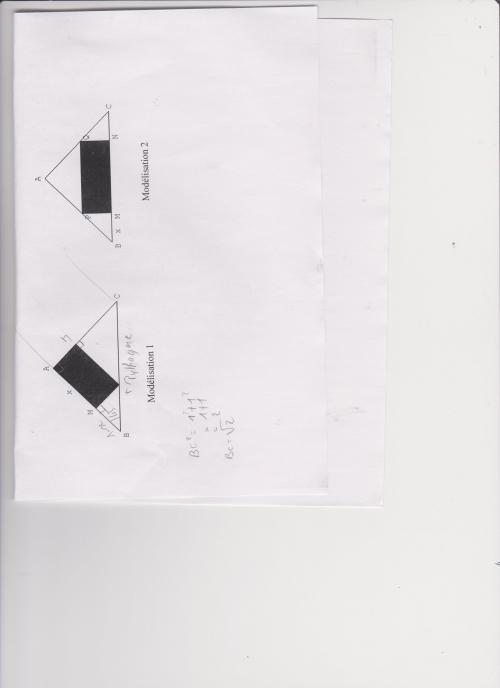
maximal (voilà le dessin du morceau de bois si besoin http://lycees.ac-rouen.fr/modeste-leroy/spip/IMG/pdf/2d4_-_dm_10.pdf)La poutre doit mesurer 10 m de longueur t sa section doit être un rectangle. On pourra placer un point libre M sur [AB] ou bien [BC] et on répondra au problème en utilisant successivement les deux modélisations ci dessous :
1 Calculer la longueur BC
BC²=BA²+AC²
1²+1²
BC= √2- Exprimer en fonction de x l'aire A(x) du rectangle noir pour la modélisation 1
- Exprimer en fonction de x l'aire B(x) du rectangle noir pour la modélisation 2
4 A l'aide de la méthode de votre choix, déterminer pour chaque cas la position de M pour laquelle l'aire est maximale et donner alors cette aire.
Je suis donc bloquée à partir de la deuxième question... Merci si vous pouviez m'aider !
-
mtschoon dernière édition par

Bonjour,
Piste,
Pour le modèle 1
A(x)=AN×NPA(x)=AN \times NPA(x)=AN×NP ( J'ai appelé P le 4ème sommet du rectangle...je ne vois pas ce qui est écrit...)
AN=x NP=BN=1−xAN=x \ NP=BN=1-xAN=x NP=BN=1−x
Tu peux donc calculer A(x)
Pour le modèle 2
B(x)=MN×PMB(x)=MN \times PMB(x)=MN×PM
MN=BC−(BM+NC)=2−(x+x)=2−2x MP=BM=xMN=BC-(BM+NC)=\sqrt 2-(x+x)=\sqrt 2-2x \ MP=BM=xMN=BC−(BM+NC)=2−(x+x)=2−2x MP=BM=xTu peux donc calculer B(x)
-
KKN dernière édition par
Merci beaucoup !
Pour la question 4 du cas 1 j'ai trouvé que l'aire maximale pour M=0.5 (abscisse du sommet de la parabole = 1+0/2) et vaut alors 0.25 (ordonnée du sommet de la parabole= A(0.5)) mais je trouve que c'est vraiment petit y a t-il une erreur ?
-
KKN dernière édition par
Et pour le cas deux je pose l'équation x√2-2x² = 0
(C'est ce que j'ai trouvé pour B(x) )
et je trouve comme solution S [0 ou 1-/-2√2)Je pense qu'il y a une erreur car pour trouver l'abscisse je ne peux pas additionner les deux solutions / 2... La solution sera un arrondi..
Donc je ne vois pas comment faire..
Merci si vous pouviez encore m'aider !
-
mtschoon dernière édition par

Je trouve tes méthodes bizarres.
Je ne sais pas ce que dit ton cours, mais, en principe, tu dois savoir que, pour f(x)=ax²+bx+c, avec a < 0, le maximum de la fonction(sommet de la parabole), est pourx=-b/2a , ce maximum étantf(-b/2a)
A(x)=−x2+xA(x)=-x^2+xA(x)=−x2+x
Le maximum de A(x) est donc pour
x=−1−2=12x=\frac{-1}{-2}=\frac{1}{2}x=−2−1=21
A(12)=14A(\frac{1}{2})=\frac{1}{4}A(21)=41B(x)=−2x2+2xB(x)=-2x^2+\sqrt 2xB(x)=−2x2+2x
Le maximum de B(x) est donc pour
x=−2−4=24x=\frac{-\sqrt 2}{-4}=\frac{\sqrt 2}{4}x=−4−2=42
B(24)=14B(\frac{\sqrt 2}{4})=\frac{1}{4}B(42)=41
-
KKN dernière édition par
Je ne connaissais pas cette formule, j'ai regardé dans mon cours
Mais cette méthode reviens au même j'ai revérifié et j'avais fais une erreur de calcul..
En fait nous posons l'équation et nous essayons de trouvé deux images "pareilles" pour ensuite les additionner et les diviser par deux pour trouver x, nous faisons ensuite f(x) pour trouver l'ordonnée
Donc merci beaucoup de votre aide !
-
mtschoon dernière édition par

De rien.
J'ignorais la méthode utilisée dans ton cours, mais elle est très bonne vu qu'elle est basée sur la symétrie de la parabole.