Devoir maison sur les angles orientés
-
Iileauxoiseaux dernière édition par
Bonjour, je cherche de l'aide pour un exercice que je ne comprend dans mon devoirs de maths. Je vous mets cette exercice ci dessous :
Je tiens a dire que j'ai des difficultés car en 3° j'ai eu une prof de maths qui partie en dépression pendant 2 mois et en seconde une remplaçante qui était toujours absente et mon lycée et au courant de ce problème car je suis évidement pas la seule dans ce cas.
C'est pour ca que j'ai du mal a comprendre. Merci de votre compréhension et de votre aide
-
mtschoon dernière édition par

Bonjour,
Ici, si tu as besoin d'aide, tu dois écrire ton énoncé à la main.
-
Iileauxoiseaux dernière édition par
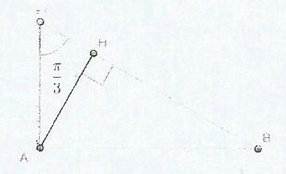
Exercie 4: Vrai ou faux? Dire pour chaque affirmation si elle est vraie ou fausse. ABC est un triangle rectangle en A tel que (vecteurCA; vecteurCB)= pi/3. Justifier.
- (vecteurBC;vecteurBA)=pi/6
2)(vecteurAB;vecteurAH)=(vecteurCA;vecteurCH)
3)(vecteurAB;vecteurCA)=pi/2
4)(vecteurAH;vecteurBA)= -pi/3
5)(vecteurAH;vecteurCB)=3pi/2
Par contre il y a une figure je fais comment pour que vous puissiez la voir ?
- (vecteurBC;vecteurBA)=pi/6
-
mtschoon dernière édition par

En dessous du cadre texte, tu dois avoir écrit :
Ajoute une imageTu cliques et tu suis ce qui est indiqué.
(ici, il faut mettre le schéma, sans le texte)
-
Iileauxoiseaux dernière édition par
-
mtschoon dernière édition par

Piste pour démarrer,
- la première affirmation est vraie.
Pour le justifier, utilise le fait que la somme des angles d'un triangle vaut ∏.
Connaissant deux angles, tu peux trouver le 3ème.- Utilise le même principe, dans le triangle ABH
Donne nous tes ébauches de calculs et nous vérifierons.
-
Iileauxoiseaux dernière édition par
Je sais que les réponses sont pour la 1) VRAI ; 2) VRAI; 3)FAUX; 4) FAUX ; 5)VRAI mais je ne sais pas comment l'expliquer

-
mtschoon dernière édition par

Avec les pistes que je t'ai données, es-tu arrivé à prouver des 2 premières propositions ?
-
Iileauxoiseaux dernière édition par
Pour la premiere j'ai fais ca : (vecteurBC;vercteurBA)= pi/2 - pi/3
= (3pi-2pi)/6=pi/6
Donc la réponse (vecteurBC;vercteurBA)=pi/6 est vrai.
Pour la deuxxieme je me melange les pinceau.
-
mtschoon dernière édition par

Prends le triangle AHB et utilise la première réponse que tu viens de trouver
A 2∏ près
(ab⃗,ah⃗)=π2−π6=...(\vec{ab},\vec{ah})=\frac{\pi}{2}-\frac{\pi}{6}=...(ab,ah)=2π−6π=...
-
Iileauxoiseaux dernière édition par
Dans le triangle ABH rectengle en H (vecAB;vecAH)=pi/2 - pi/6= (6pi-pi)/6= 5pi/6
Dans le triangle ABC rectangle en A pi/3 + pi/6 + pi/2= (4pi+2pi+6pi)/12=12pi/12=pi or on sait que la somme des trois angles d'un triangle vaut pi
voila ce que j'ai trouver pour la question 2
-
mtschoon dernière édition par

Tu as écrit :
Citation
Dans le triangle ABH rectengle en H (vecAB;vecAH)=pi/2 - pi/6= (6pi-pi)/6= 5pi/65∏/6 est faux . Refais ton calcul et tu auras la réponse (exacte) à la 2.
-
Iileauxoiseaux dernière édition par
A la 3) j'ai trouve : (vecAB;vecCA) = pi/2 est fausse car (vecAB;vecCA)= (vecAB;vecAH)+(vecAH;vecHC)+(vecHC;vecCA)=pi/2+(vecAH;vecHA)+(vecHA;vecHC)+(vecHC;vecCH)+(vecCH;vecCA) = pi/2 + pi - pi/2 + pi - pi/3= (3pi + 6pi - 3pi + 6pi - 2pi)/6=10pi/6
-
Iileauxoiseaux dernière édition par
a la 4) J'ai trouve ca : (vecAH;vecBA)=(-pi)/3 et fausse car (vecAH;vecBA)= (vecAH;HA)+(vecHA;vecBA)= pi + (vecHA;vecAH) + (vecAH;vecBA) + (vecBA;vecAB) = pi + pi + (vecAH;vecBA)+ pi = 3p i+ (vecAH;vecBA) + 2kpi
-
mtschoon dernière édition par

Tu comptes très bizarrement...
A 2∏ près :
Pour la 2:
(ab⃗,ah⃗)=π2−π6=3π6−π6=2π6=π3(\vec{ab},\vec{ah})=\frac{\pi}{2}-\frac{\pi}{6}=\frac{3\pi}{6}-\frac{\pi}{6}=\frac{2\pi}{6}=\frac{\pi}{3}(ab,ah)=2π−6π=63π−6π=62π=3π
Pour la 3:
(ab⃗,ac⃗)=π2(\vec{ab},\vec{ac})=\frac{\pi}{2}(ab,ac)=2π donc
(ab⃗,ca⃗)=−π2(\vec{ab},\vec{ca})=-\frac{\pi}{2}(ab,ca)=−2πPour la 4:
Tu sais que (ab⃗,ah⃗)=π3(\vec{ab},\vec{ah})=\frac{\pi}{3}(ab,ah)=3π
Tu peux en déduire logiquement la valeur de (ah⃗,ba⃗)(\vec{ah},\vec{ba})(ah,ba)
-
Iileauxoiseaux dernière édition par
Ah oui au lieu de mettre 3 j'ai mit 6 -_- merci mais alors est juste ?
et la 3 elle est bien fausse ?
Et la 4 est fausse aussi ?
a la cinq j'ai trouve ca : Et a la derniere question je trouve ca : (vecAH;vecHC) + (vecHC;vecCB) =(vecAH;vecHA) + (vecHA;vecHC) + (vecHC;vecCH) + (vecCH;vecCB) = pi - pi/2 + pi (car (vecCH;vecCB) = pi/2 + pi/2 = 2pi/2 = pi) + pi = 3pi - pi/2 mais a partir de la je bloque car je ne sais pas si la reponse et fausse ou vrai a la question 5) par rapport a mon calcul
-
mtschoon dernière édition par

Effectivement ,les deux premières sont vraies et la 3) est fausse.
Pour la 4), calcule l'angle et tu sauras si la proposition est vraie ou fausse.
-
Iileauxoiseaux dernière édition par
Comme justification pour la reponse 1 est ce que ca va: (vecteurBC;vercteurBA)= pi/2 - pi/3
= (3pi-2pi)/6=pi/6
Donc la réponse (vecteurBC;vercteurBA)=pi/6 est vrai.Comme justification pour la reponse 2 est ce que ca va: (vecAB;vecAH) = pi/2 - pi/6 = (3pi - pi ) /6 = 2pi /6 = pi/3 Donc la reponse a (vecAB;vecAH)= (vec CA;vecCH) est vraie
Comme justification pour la reponse 3 est ce que ca va: (vecAB;vecAC) = pi/2 donc (vecAB;vecCA) = - pi/2 donc la reponse a (vecAB;vecCA) = pi/2 est fausse
(vecAH;vecBA) = -pi/3 est fausse car (vecAH;vecAB) = -pi/3 donc (vecAH;vecBA) = pi/3 donc la reponse a (vecAH;vecBA)=-pi/3 est fausse
est ce que ca va si je les justifie comme cela ?
pour la cinq j'ai fait ca : Et a la derniere question je trouve ca : (vecAH;vecHC) + (vecHC;vecCB) =(vecAH;vecHA) + (vecHA;vecHC) + (vecHC;vecCH) + (vecCH;vecCB) = pi - pi/2 + pi (car (vecCH;vecCB) = pi/2 + pi/2 = 2pi/2 = pi) + pi = 3pi - pi/2 mais a partir de la je bloque car je ne sais pas si la reponse et fausse ou vrai a la question 5) par rapport a mon calcul
-
mtschoon dernière édition par

Tes textes sont difficiles à lire !
Pour la 4), tu devrais trouver :
(ah⃗,ba⃗)=(ah⃗,ab⃗)+(ab⃗,ba⃗)=−π3π+π3=2π3(\vec{ah},\vec{ba})=(\vec{ah},\vec{ab})+(\vec{ab},\vec{ba})=-\frac{\pi}{3}\pi+\frac{\pi}{3}=\frac{2\pi}{3}(ah,ba)=(ah,ab)+(ab,ba)=−3ππ+3π=32π (à 2∏ près)
La proposition est donc fausse
Revois tes calculs si besoin.
-
Iileauxoiseaux dernière édition par
Desole de mal m'exprimer mais je ne sais pas faire les vecteurs, les pi, les fractions comme vous

-
Iileauxoiseaux dernière édition par
J'ai beau essaye mais soit je retrouve toujours le meme calcul soit je trouve des nombre trop grand
 et pour la 5 je sais que c'est vrai mais ca me fait le meme probleme que la 4)
et pour la 5 je sais que c'est vrai mais ca me fait le meme probleme que la 4) 
En revanche pour les questions 1 a 3 elles sont bien et justes ?
-
mtschoon dernière édition par

Au lieu de te perdre dans les calculs, essaye de regarder avec soin le schéma.
Pour la 5)
(ah⃗,bc⃗)=π2(\vec{ah},\vec{bc})=\frac{\pi}{2}(ah,bc)=2π (à 2∏ près)
donc:
(ah⃗,cb⃗)=(ah⃗,bc⃗)+(bc⃗,cb⃗)=π2+π=3π2(\vec{ah},\vec{cb})=(\vec{ah},\vec{bc})+(\vec{bc},\vec{cb})=\frac{\pi}{2}+\pi=\frac{3\pi}{2}(ah,cb)=(ah,bc)+(bc,cb)=2π+π=23π (à 2∏ près)
-
Iileauxoiseaux dernière édition par
Ah oui j'avais oublie qu'il fallait mettre au meme denominateur-_-
Pour la deux si je mets que ca (vecAB;vecAH) = pi/2 - pi/6 = (3pi - pi ) /6 = 2pi /6 = pi/3 Donc la reponse a (vecAB;vecAH)= (vec CA;vecCH) est vraie ca va ????
-
mtschoon dernière édition par

oui.
-
Iileauxoiseaux dernière édition par
Je comprend pas d'ou vient le π a côté du -π/3: (\vec{AH},\vec{BA})=(\vec{AH},\vec{AB})+(\vec{AB},\vec{BA})=-\frac{\pi}{3}\pi+\frac{\pi}{3}=\frac{2\pi}{3} (à 2∏ près)
-
Iileauxoiseaux dernière édition par
(vecAH;vecBA)=(vecAH;vecAB)+(vecAB;vecBA)=-π/3π + π/3= 2π/3 +2kπ
-
mtschoon dernière édition par

(ab⃗,ba⃗)=π(\vec{ab},\vec{ba})=\pi(ab,ba)=π (à 2∏ près)