Configuration du plan

Bonjour à tous !
J'ai besoin d'aide pour un DM sur la configuration du plan : on m'a donné une figure à construire sur géogebra (un quadrilatère EFGH dans un quadrilatère ABCD)

la première question était :Conjecturer la nature de EFGH. J'ai répondu que c'était un parallélogramme selon la propriété des milieux seulement, ensuite on me demande :

Démontrer que (EF) et (GH) sont parallèles puis qu'il en est de même pour (HE) et (FG)
et là je bloque parceque je ne sais pas si je peux utiliser Thalès ( avec quelles valeurs ?) ou les propriétés du parallélogramme car je n'ai pas la certitude que c'en est bien un...
De l'aide s'il vous plait !!

Bonjour,

Comment veux-tu qu'on t'aide sans en savoir plus sur la façon dont on place les points E , F , G et H ????

effectivement c'est peu logique désolée xD
Voilà la figure pour visualiser..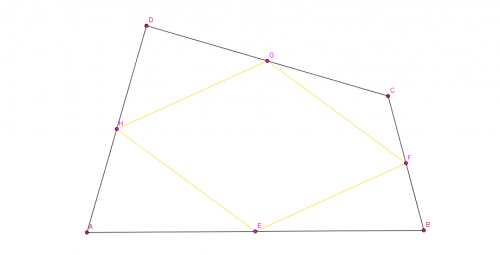

voici la figure en question

Et ils sont placées au hasard sur les côtés du quadrilatère ABCD ?

On va vraiment avoir du mal à t'aider si tu nous distilles les info au compte goute !

Non. Un exercice nous a été donné et dans l'énoncé de celui-ci il y avait cette figure la première question était "Faire cette figure avec un logiciel de géométrie" . Donc la figure est comme ça, c'est pour la suite que je bloque . Ce que je demande ne me paraissait pas si mal expliqué.

Bonjour,

Je me permets une petite réflexion en attendant que Zorro soit là pour te répondre.

Pour que l'énoncé ait un sens ( EFGH parallélogramme) , il faut que les points E,F,G,H aient des positions très particulières.
Visiblement, vu le schéma que tu donnes, ces points sont les milieux des côtés.

Dans la première question, tu n'a pas de justification à donner : on te demande uneconjecture : tu dois "deviner" graphiquement la nature du quadrilatère EFGH.

La question 2) te fait démontrer mathématiquement ce que tu as précédemment deviné.

Piste pour les démonstrations:

Trace (AC) et (BD) et ensuite, en fonction de tes connaissances, utilise les droites des milieux des triangles ou la réciproque du théorème de Thalès appliqué aux triangles.

Zorro t'aidera, si besoin, lorsqu'elle sera là.

d'accord je vous remercie ! je vais faire ça.
Par contre, c'est idiot comme question, mais si je choisi le théorème de Thalès pour démontrer, je n'ai pas de mesures indiquées dans l'énoncé donc je ne sais pas si je dois moi même les définir ou non... :frowning2:

Attention : il ne s'agit pas du théorème de Thalès mais de sa "réciproque appliquée aux triangles".

Il ne faut pas donner de mesures, sinon ta démonstration ne serait pas générale.

Mais, c'est tout simple.
un exemple :
Si I est le milieu d'un segment [AB],$\text{ \frac{AI}{AB}=\frac{AI}{2AI}=...$

d'accord je vois à peu près, donc là en l'occurrence on a E milieu du segment [AB]..mais pour le quadrilatère EFGH, cela suffit à prouver que (EF) et (GH) sont parallèles ?

attention !

il faut démontrer avec rigueur !

prends le temps de réfléchir...

oui, j'ai beaucoup de mal =(
bon je vais essayer de comprendre avec les propriétés, merci quand même de votre aide !

Je t'ai donné un indice : trace les droites (AC) et BD) : elles sont utiles aux démonstrations.

(AC) sera utile pour arriver à prouver avec rigueur que (EF)//(HG)
(prouve que (EF)//(AC) et que (HG)//(AC) donc...)

(BD) sera utile pour arriver à prouver avec rigueur que (HE)//(GF)
(même principe)

Tu pourras nous faire part de ton raisonnement

Zorro, si elle est là, te dira s'il est bon

oui c'est ce qui est si compliqué. Le théorème des Milieux semble plus efficace non ?
j'ai pu prouver grâce à lui que (HG) // (AC) et donc que (EF)//(AC) !
Pour la suite, faut-il une nouvelle propriété ?

Fais de la logique !

Ce "donc que" que tu écris n'est pas bon.

Tu dois démontrerséparément que :
(HG)//(EC)
(EF)//(AC)

Ensuite, lorsque deux droites sont parallèles à une même troisième, elles sont parallèles entre elles .

Les droites (HG) et (EH) sont toutes deux parallèles à (AC), donc elles sont parallèles entre elles :
donc (HG)//(EF)

Super ! Je vais mettre tout ça au propre, merci beaucoup pour vos explications.
Ensuite on me demande "quelles propriétés doivent avoir les diagonales du quadrilatères ABCD pour que EFGH soit un rectangle, un losange ou un carré ?"
Ici il suffit simplement de trouver les propriétés des diagonales de chacuns de ces quadrilatères c'est ça ?

N'oublie pas de démontrer aussi que (EH)//(GF)

Ainsi, tu auras bien démontré que EFGH est un parallélogramme

Pour ta dernière question , effectivement, on te demande d'étudier des cas particuliers

Lorsque EFGH est un rectangle, que peut-on dire de (AC) et (BD)?
Lorsque EFGH est un losange, que peut-on dire de (AC) et (BD)?
Lorsque EFGH est un carré, que peut-on dire de (AC) et (BD)?

A toi de faire.

En effet, il aurait fallu coder le fait que E est le milieu de [AB] , etc ....

Et il faut bien utiliser plusieurs fois le théorème de la droite des milieux en précisant à chaque fois, dans quel triangle tu l'appliques

Dans le triangle ... , ? est milieu de [??] , ??? est milieu de [????] donc d'après le théorème de la droite des milieux , les droites (..) et (..) sont parallèles ...

Et tu vas y arriver en raisonnant de façon logique.

je pense que je vais pouvoir achever mon DM avec tout ça ! Je vous remercie toutes les deux pour vos aides !
Cordialement

De rien et à bientôt si tu as encore besoin de nous, ou à jamais si tu arrives à faire tes exercices sans nous.

je pense plutôt à bientôt ^^ au revoir !