Résolution problème d'optimisation surface de baignade via les fonctions

Bonjour à tous !

Voilà, je bloque sur un problème ouvert que j'essaie de résoudre depuis quelques temps déjà, je sais que c'est un "classique", mais je n'y arrive pas...
Voici l'énoncé:

I/ Optimisation de la surface de baignade

Un maître-nageur dispose d'une corde de 55m de longueur pour délimiter un rectangle de baignade surveillée de forme rectangulaire. Il souhaite obtenir une aire maximale. Comment disposer la corde ?

C'est mon premier problème ouvert, il y a un autre exercice avec celui-ci mais j'ai lu qu'il ne fallait poster qu'un exercice à la fois.

Je pense qu'il faut utiliser la forme canonique, mais je ne sais pas comment faire...

Merci d'avance pour votre aide !

Bonjour,

Piste pour démarrer,

Si j'ai bien compris l'énoncé, la corde de 55m fait la ligne AB-BC-CD composée de 3 segments ( en rouge sur mon schéma)

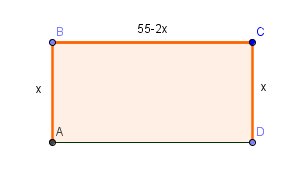
$fichier math$

Tu peux poser AB=x ( avec la conditionx ≥ 0)

donc AB+BC+CD=55 <=> x+BC+x=55 <=> BC=55-2x

condition 55-2x ≥ 0 <=> x ≤ 55/2

L'aire du rectangle vaut donc :

$\text{aire(ABCD)=f(x)=AB\times BC=x(55-2x)=-2x^2+55x$

Tu dois donc étudier les variations de f sur [0 , 55/2] pour en déduire le maximum

Merci beaucoup ! Je pense que ça va bien m'aider:)

De rien ( et tu dois trouver 55/4 )