Montrer une inégalité avec des distances

Bonjour, alors voilà j'ai un petit souci en ce qui concerne la deuxième partie d'un exercice, alors j'aimerais un peu d'aide j'ai commencé quelques petits trucs mais je ne sais pas si je suis sur la bonne route :).
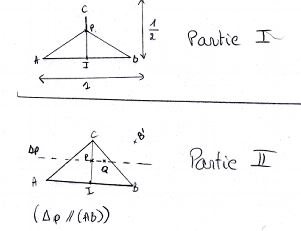
1ère partie: (CI) la médiatrice du segment [AB], AB=1 et CI=1/2 (comme sur le dessin) Il s'agissait de placer un point P sur la médiatrice (IC) de tel sorte que L=AP+BP+CP soit minimale. Et de dire par la suite quelle était la valeur de l'angle PAI.
J'ai fait tout cette partie là en posant IP=x ensuite en me servant d'une fonction $ap+bp+cp=2×x2+14+12−xap+bp+cp=2\times\sqrt{x^2+\frac{1}{4}}+ \frac{1}{2}-x$ que j'ai étudié sur l'intervalle [0;1/2] pour trouver son minimum qui était $112\frac{1}{\sqrt{12}}$ . l'angle ensuite j'ai trouver 30°.

Maintenant je bloque pour la deuxième partie de l'exercice, je fais un dessin pour que sa soit plus explicite.
Le but est alors de montrer que AP+PB<AQ+BQ. Et ainsi que AP+BP+CP<AQ+BQ+CQ.
Pour ça j'ai fait le symétrique de B par rapport à ∇P. Et sa fait que APB' sont alors alignés et c'est donc le plus court chemin mais ça je le vois graphiquement donc je ne sais pas si c'est juste. j'aimerais donc un petit coup de main

Enfin la dernière partie la question est:
Ou faut-il placer le point P dans le triangle ABC pour que L=AP+BP+CP soit minimale. Je n'en ai aucune idée

Voilà je vous remercie d'avance pour votre aide. $fichier math$

Bonjour,

Les résultats de ta première partie sont bons.
Cependant, si j'ai bien lu, tu as pris $cp=12−xcp=\frac{1}{2}-x$

Cela sous-entant que P est nécessairement que P est entre C et I. Je suppose que tu l'as justifié.

Tu devrais recopier exactement l'énoncé de la seconde partie (sans tes interprétations personnelles) .
Le dessin, c'est bien, mais il faut connaître l'énoncé de base, pour ne pas faire d'erreur d'interprétation.

Bonjour, merci pour votre réponse alors je recopie l'énoncé:
Montrer que AP+PB<AQ+QB puis que AP+PB+PC<AQ+QB+CQ.

Ou faut-il placer P dans le triangle ABC pour que L=AP+BP+CP soit minimale?

Et en plus on a la figure que j'ai fait dans le premier post voilà

Je ne suis guère plus avancée...Si tu n'as rien d'autre, il faut faire avec le schéma que tu donnes pour la question 2...mais un schéma n'est qu'une une image fixe qui doit illustrer un texte, mais ne doit pas le remplacer.

Dans le cas du schéma, c'est à peu près "évident"

QA+QB=QA+QB'
PA+PB=PA+PB'=AB'

Or, AB' < QA+QB' (la ligne droite est le plus court chemin entre deux points - tu peux parler d'inégalité triangulaire -)

Donc :

PA+PB < QA +QB

Vu que QC > PC (dans un triangle rectangle, l'hypoténuse est supérieure aux côtés de l'angle droit), tu obtiens finalement :

PA+PB +PC < QA +QB + QC , c'est à dire L < QA +QB + QC

La fin se ramène à la question précédente.