Problèmes fonctions

Bonsoir,

J'ai un exercice à faire, mais je n'ai pas bien compris, j'ai tout de même essayer de le faire, mais j'ai vraiment besoin d'aide. Voici l'énoncé :

ABCDEFGH est un cube d'arête 4 cm. Pour tout point M de [AB] on construit le point N de [AD] tel que DN=AM.
On note x= AM (cm)
Les droites (MP) et (NR) sont parallèles à (AE).

Exprimer le volume de V(x) du solide MBCDNPFGHR en fonction de x.
Puis justifier que V admet un minimum sur [0;4]. Préciser ce minimum et pour quelle position de M il est atteint.

MES REPONSES :

V(ABCDEFGH) = Lxlxh = 444 = 64 cm $^3$
V(AMNEPR) = Aire Base x H = (xAN)/2x4
V (MBCDNPFGHR) = V(ABCDEFGH)-V(MBCDNPFGHR) = 64-(xAN/2x4)

Ensuite je suis bloqué, de plus je ne sais pas si mon raisonnement est juste...
Quelqu'un peut m'aider ?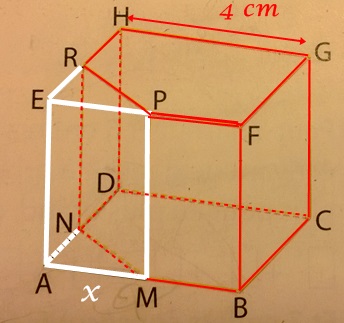

Voici le schéma

Bonjour,

Je pense que c'est AN qui te bloque.

Pour 0≤x≤4 , AN=4-x

$\text{V(AMNEPR)=(Aire Base) fois H=\frac{(xAN)}{2}\times 4=\frac{x(4-x)}{2}\times 4$

$\text{V(AMNEPR)=2x(4-x)=8x-2x^2$

V cube- Vprisme = 64-(-2x²+8x)

oui.

En développant

$V(x)=64+2x^2-8x$

En ordonnant les termes :

$V(x)=2x^2-8x+64$

Pour x ∈ [0, 4] , V(x) est un polynôme du second degré dont tu détermines le minimum

a= 2
b= -8

On applique : -b/2a = X
-8/2*2 = X
X= 2 ?

Est-ce que je dois faire un intervalle ou j'exclue 2 ?

Citation
Est-ce que je dois faire un intervalle ou j'exclue 2 ?
Phrase très bizarre...

Si ton cours te dit que pour un polynôme de la forme ax²+bx+c avec a > 0, le minimum est pour x=-b/(2a),x=2 est la valeur de x pour laquelle V(x) est minimale.

Comme cette valeur est dans [0,4] ( intervalle d'étude), elle convient.

Ok, merci beaucoup !

De rien !