Espace volumes

Bonjour !

Je fais le dernier exercice de mon dm, et encore un petit problème : je ne sais pas comment le résoudre...

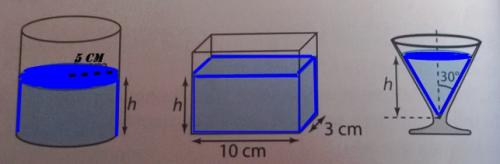
Enoncé : On verse une même hauteur h de liquide (en cm) dans chacun des récipients suivant (voir la photo)

Question : Quel récipient contiendra le plus de liquide ?

Je pense qu'il faudrait trouver le volume du liquide, et la hauteur pour en déduire le volume d'eau que contient le solide mais je ne sais pas si c'est juste...J'ai commencé mais je suis bloqué :
Solide 1 - V= Aire Base x H
Aire de la base = 31, 4 environ
donc ---> V= 31,4 x H

Solide 2 - ABxH
V= 30 x H

Solide 3- V= ABxH/3 mais pour celui-ci je suis encore plus bloqué...

Quelqu'un peut m'aider ?

$fichier math$

Bonjour,

Rappel : l'aire d'un disque de rayon R est ∏R²

Quelques pistes,

Revois l'aire de la base du solide 1 , en utilisant la propriété que je viens de t'indiquer. Je pense que tu as confondu la formule de l'aire avec celle du périmètre.

Oui pour le solide 2

Pour le solide 3 , il faut trouver le rayon R de la "base" en utilisant la définition de la tangente d'un angle aigu dans un triangle rectangle

tan(30°)=R/h donc R=htan(30°)

base=∏R²

ensuite , tu utilises la formule du volume : (1/3)xbasexh

Donc :

Solide 1 : Aire = 25∏ environ 78,5 cm

Solide 3 : tan(30) = √3/3
---> Aire = ∏x√3/3² = 1/3∏
Donc V = 1/3x1/3∏xh ?

Oui pour solide 1

Pour le solide 3 , les "h" ont disparu.

Vérifie.

Tu dois trouver :

$V3=19πh3V_3=\frac{1}{9}\pi h^3$

S1 = Aire : 78,5 cm²
S2 = Aire : 30 cm²
V3 = 1/9∏ $h^3$

Mais Comment trouver h et savoir quel solide en contient le plus ?

h ne prend pas une valeur précise.

Tu as :

$V3=π9h2hV_1=25\pi h \ V_2=30h \ V_3=\frac{\pi}{9}h^2h$

Pour savoir quel est le volume maximal, il faut comparer ces 3 volumes.

Déjà $V2<V1V_2\lt V_1$

Donc $V_2$ ne peut pas être le volume maximal.

Il reste à comparer $V_3$ et $V_1$

Tu peux faire une discussion, suivant h

Tu cherches
dans quel cas $V_1$ < $V_3$
dans quel cas $V_1$ = $V_3$
dans quel cas $V_1$ > $V_3$

Dans chacun de ces cas, tu pourras déduire quel est le volume maximal.

J'ai rentré V1 et V2 dans ma calculatrice pour tracer les courbes mais je ne trouve aucune valeur où V1
v3
V1= 314,16
V3= 22,34

Aucune valeur où V1<V3 et V1=V3
mais seulement : V1 = 314,16
V3 = 22,34
Donc le solide 3 contient le plus de liquide ?

Le solide 1 je veux dire

Il faut régler la fenêtre de ta calculette graphique judicieusement pour pouvoir "voir" la réponse...

Si "h" s'appelle x sur ta calculette , pour "windows", choisis par exemple :

xmin=0
xmax=25
ymin=0
ymax=2000

Mais, "voir" n'est pas suffisant, il faut faire les démonstrations mathématiques.