Calcul des coordonnées d'un point en utilisant la fonction inverse

Bonjour, j'ai un devoir à rendre pour le 28/04. J'ai cherché pendant plusieurs heures sans trouver grand chose :frowning2:

Voici l'énoncé :

Dans un repère orthonormé (O, I, J), A est le point de coordonnées (0 ; -1) et M un point distinct de O, qui décrit l'axe des abscisses (d'ordonnée fixe 0).
On note x l'abscisse du point M.

La parallèle à la droite (AM) passant par I coupe l'axe des ordonnées en N (N est d'abscisse fixe 0).
H est le point tel que OMHN est un rectangle.

Démontrer que le point H a pour coordonnées (x ; (-1)/x).

Voici la figure :

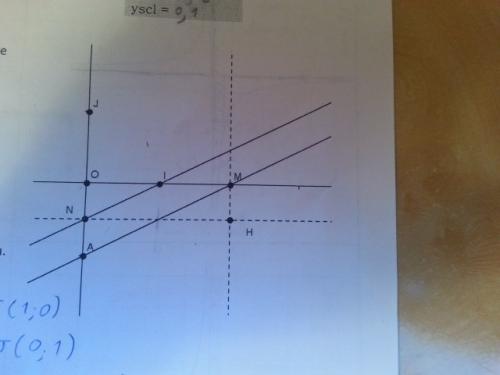
$fichier math$

J'ai simplement remarqué que yH = yN pour toutes les valeurs de x.

En espérant que vous pourrez m'aider :rolling_eyes:

Bonjour,

(AM)//(NI)

Avec le théorème de Thalès appliqué aux triangles, en utilisant les mesures algébriques :

$ON‾OA‾=OI‾OM‾\frac{\overline{ON}}{\overline{OA}}=\frac{\overline{OI}}{\overline{OM}}$

$ON‾−1=1x\frac{\overline{ON}}{-1}=\frac{1}{x}$

Donc

$ON‾=−1x\overline{ON}=-\frac{1}{x}$

Donc

$y_H=.....$

N'ayant jamais vu les mesures algébriques en cours bien que je comprenne ce que vous avez écrit, ma professeure ne va peut-être pas accepter cette réponse. Y a-t-il un autre moyen ?

En tout cas merci de votre réponse

Si tu ne dois pas utiliser les les mesures algébriques, tu peux travailler en deux temps

Tu utilises d'abord le théorème de Thalès avec les distances.

Tu obtiendras

$ON=∣yN∣=1∣x∣ON=|y_N|=\frac{1}{|x|}$

Ensuite, tu justifies que $y_N$ et x sont de signe contraire, d'où

$yN=−1xy_N=-\frac{1}{x}$

Comment puis-je justifier cela et que signifient les deux traits autour de yN et de x ?

Il s'agit des valeurs absolues.

Merci beaucoup. J'ai fait :

(AM)//(NI)
N ∈ (OA)
I ∈ (OM)

D'après le théorème de Thalès, les triangles OIN et OMA ont des longueurs proportionnelles. On a donc :

$OIOM=ONOA\frac{OI}{OM}=\frac{ON}{OA}$ ⇔ $∣1∣∣x∣=ON∣1∣\frac{|1|}{|x|}=\frac{ON}{|1|}$

ON = |1| * |1| / |x|

ON = |1/x| = |yN|

(MA)//(IN), yA < 0 et xI > 0

si xM > 0, xN < 0
si xM < 0, xN > 0 (cela suffit-il à justifier que yN et xM = x sont de signes contraires ?)

D'où yN = -(1/x)

Puisque OMHN est rectangle, xM = xH et yN = yH. Le point H a donc pour coordonnées (xM ; yN), soit (x ; -(1/x)).

Est-ce correct ?

Cela semble correct , mais |1|=1 : mets 1 directement (sans valeur absolue)

Evidemment, sans l'utilisation des mesures algébriques, cette méthode est bien lourde.

Une autre possibilité si tu connais les vecteurs.

Tu peux dire, vu le parallélisme, qu'il existe un réel k que :

$\left{\vec{OM}=k\vec{OI}\ \vec{OA}=k\vec{ON}\right$

En prenant l'égalité des abscisses pour la première relation et celle des ordonnées pour la seconde, tu obtiens :

$\left{x_M=kx_I\ y_A=ky_N\right$

$\left{x_M=k\ -1=ky_N\right$

Tu obtiens ainsi :

$1=x_M y_N$

D'où :

$yN=−1xMy_N=\frac{-1}{x_M}$

A toi de voir ce qui s'adapte le mieux à ton cours.

J'ai opté pour la solution avec les vecteurs.

Merci de m'avoir consacré de votre temps pour m'aider

De rien.

A+