Montrer des égalités en s'aidant du cercle trigonométrique

Bonjour !

Partie 1 :

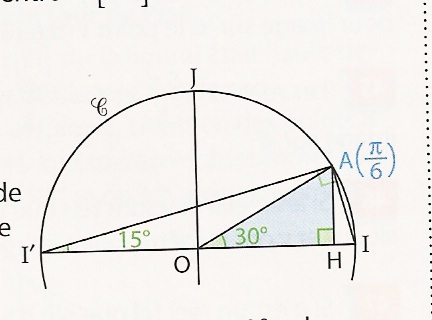
A est le point image du réel π/6 sur le cercle trigonométrique C de centre O. [AH] est la hauteur du triangle IAI'.

Justifier les mesure 30° et 15° indiquées sur la figure.
a) Montrer que AI' = 2cos15° et en déduire AH en fonction de cos15° et sin15°
b) Déduire une relation simple entre sin 30° et le produit sin15° * cos15°
Répondre à la question posée dans le titre.

Où j'en suis :

J'ai répondu à tout et je suis au 2. b) Je n'arrive pas à prouver que sin(2*15°) = 2 * sin(15°)

J'ai réussi à démontrer que sin(2 * 15°) = 2cos(15°) * sin(15°)

Partie 2 : Valeurs exactes de sin(π/12) et π(cos/12)

Déterminer la valeur exacte de I'H.

2.a Exprimer de deux façons cos15), en se plaçant dans les triangles I'AH et I'AI.
b. En déduire que I'H=2(cos15°)²

Déduire des questions 1 et 2 la valeur exacte des cos15°
Déterminer alors celle de sin15°
En déduire les valeurs du titre de l'exercice.

Merci d'avance ! $fichier math$

Bonjour,

Dans la partie 1), sin(2*15°) ≠ 2 * sin(15°) ( la fonction sinus n'est pas linéaire, alors tu ne risques pas démontrer l'égalité, car elle est fausse)

Piste pour la partie 2)

I'H=I'O+0H=1+cos(30°)=1+√3/2

Tu peux écrire : $I′H=2+32I'H=\frac{2+\sqrt 3}{2}$

Essaie de poursuivre.

C'est bon j'ai réussi en fait. Je suis à la question 3 de la partie 2 où je ne sais pas comment y aller...

Sinon pour la partie 2) Question 2.a., la réponse est uniquement
cos(15) = I'H / I'A
cos(15) = I'A / II'

ou il faut que j'aille plus loin ?

C'est bon pour la 2)a) . Tu peux remplacer II' par 2

Si tu as fait la 2)a) puis la 2)b) , la 3) est une simple conséquence.

Avec la 2)b), tu peux isoler (cos15°)²

Il te reste à remplacer I'H par l'expression trouvée au 1)

Ensuite, tu prends la racine carrée pour obtenir cos15°

J'avais déjà réussi pour le 2.b. mais je ne sais pas comment approcher le 3...

Je te répète ce que je viens de t'écrire :

" Avec la 2)b), tu peux isoler (cos15°)²

Il te reste à remplacer I'H par l'expression trouvée au 1)

Ensuite, tu prends la racine carrée pour obtenir cos15°"

J'ai réussi à tomber sur ça :

cos(15) = √[2cos(30) + 2] / 2

C'est ça ?

Oui, c'est ça, mais remplace cos(30) par sa valeur exacte ( $sqrt32\frac{sqrt 3}{2}$ )

C'est bon, j'ai fini cet exercice, mais je n'arrive pas à faire celui-ci, pourriez-vous m'aider ? http://www.mathforu.com/sujet-21989.html

Merci d'avance !

Pour ton second sujet, je vois que Noemi t'a répondu, donc pas de problème .

Bon DM.