Résoudre un problème à l'aide des formules sur les suites

Bonjour tout le monde, je suis bloqué sur un exercice sur les suites...
Voici l'énoncé :

Etape 0 : On commence avec un carré de côté 1.
Etape 1 : On le divise en 9 carrés et on noircit celui du centre.
Etape 2 : On prends les 8 carrés restants et on les divise en 9 carrés. On noircit les 8 carrés centraux.
Etape 3 : De l'étape précédente, il reste 64 carrés non noircis. On les découpe en 9 carrés chacun et on noircit la carré central.
Et continue jusqu'à la fin des temps! Voir le dessin

A partir de l'étape 1, on appelle :
Cn le nombre de carrés noircis qui apparaissent à l'étape n (on ne compte pas les précédents).
Pn le côté de chacun de ces carrés.
On voit que :
C1 = 1; P1 = $13\frac{1}{3}$ ; C2 = 8; P2 = $19\frac{1}{9}$ ; c3 = 64 et P3 = $127\frac{1}{27}$

On devine une formule donnant Cn+1 en fonction de Cn et une formule donnant Pn+1 en fonction de Pn.
a. Justifier ces formules
b. En déduire des formules donnant Cn et Pn en fonction de n. Vérifier que les formules sont cohérentes avec les premiers termes calculés à partir du dessin.
a. Calculer les sommes
Pn = 4(C1P1 + C2P2 + .... + CnPn)
Sn = C1(P1)² + C2(P2)² + ... + Cn(Pn)²
b. Que représentent-elles sur le dessin?
c. Quelles sont leurs limites quand n devient très grand?
d. Quel objet bizarre a-t-on ainsi créé?

Je n'arrive pas à mettre le dessin, la taille est trop grande je ne comprends pas...
Pour la question 1 j'ai trouvé que Cn+1 = 8 x Cn => Cn = 1 x 8^n et que Pn+1 = $13\frac{1}{3}$ x Pn => Pn = $13\frac{1}{3}$ x $13\frac{1}{3}$ ^n
Est-ce bien ça?
J'aurais aussi besoin d'aide pour la question 2), je n'y arrive vraiment pas...
Merci d'avance!

Bonjour,

Pour le dessin, avec ton scanner tu aurais pu peut-être faire une réduction avant d'enregistrer pour pouvoir mettre l'image.

J'ai fait un schéma avec les deux premières étapes.
Merci de dire si c'est bien ce qu'il fallait comprendre.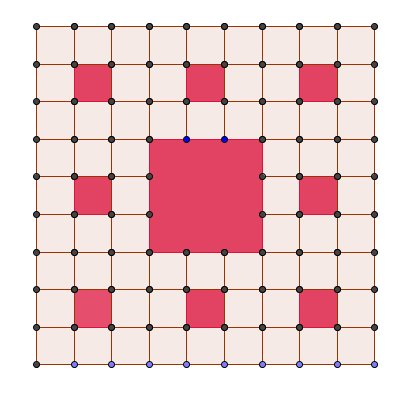

$fichier math$

Si c'est bien ça, conjectures

$\text{c_1=1\ p_1=\frac{1}{3} \ c_2=8\ p_2=(\frac{1}{3})^2=\frac{1}{9} \ c_3=8^2=64\ p_3=(\frac{1}{3})^3=\frac{1}{27} \ c_4=8^3\ p_4=(\frac{1}{3})^4 \ ... \ c_n=8^{n-1}\ p_n=(\frac{1}{3})^n$

Pour le dessin c'est exactement ça, je vais essayer de le scanner du coup!

$fichier math$

Effectivement je m'étais trompé sur Cn et Pn, merci!
Du coup je ne comprends pas comment on calcule la somme Pn et Sn dans le 2)
Pour Pn, comme c'est une suite arithmétique, on fait avec la formule :
4 x $1−qn+11−q\frac{1-q^{n+1}}{1-q}$ ou 4 x $qn+1−1q−1\frac{q^{n+1}-1}{q-1}$ mais je ne vois pas qui est "q" et comment on fait vu qu'on ne connait pas "n"?

$P_n$ ) n'est pas une suite arithmétique

Bilan sur ce que tu aurais dû trouver à la 1)

$C_n$ ) suite géométrique de premier terme $C_1$ =1 et de raison q=8

d'où $c_n=c_1q^{n-1}=...$

$P_n$ ) suite géométrique de premier terme $P_1$ =1/3 et de raison Q=1/3

d'où $p_n=p_1q^{n-1}=...$

Pour la 2)a) commence à changer les notations.Quelque chose ne va pas...

Citation
Pn = 4(C1P1 + C2P2 + .... + CnPn)

Ensuite, avant de calculer les sommes, il faut trouver la nature de la suite $(C$ _n $P_n$ ) et de la suite $(C$ _n $P_n$ ²)

Oui je me suis trompé, j'ai marqué arithmétique sans le vouloir...
Pour Cn et Pn j'avais trouvé comme toi sauf que je m'étais trompé dans le puissance.
Pour le 2)a. c'est bien ce que j'ai mis :
$pn=4(c1p1+c2p2+...+cnpn)p_{n} = 4\left(c_{1}p_{1} + c_{2}p_{2}+ ... + c_{n}p_{n} \right)$

Quand tu dis "nature de la suite" c'est savoir si elle est géométrique ou arithmétique? Si c'est le cas, $c_{n}p_{n}$ est géométrique non?
$cnpn=8n−1(13∗13n−1)c_{n}p_{n} = 8^{n-1} \left(\frac{1}{3}* \frac{1}{3}^{n-1} \right)$
c'est bien ça?
Si oui, $13∗13n−1=13n\frac{1}{3} * \frac{1}{3}^{n-1} = \frac{1}{3}^{n}$ non?

Donc $cnpn=8(n−1)∗13nc_{n}p_{n} = 8(^{n-1}) * \frac{1}{3}^{n}$ ?

J'ai essayé de te dire qu'une notation ne va pas...

Tu as écrit
$p_{n} = 4\left(c_{1}p_{1} + c_{2}p_{2}+ ... + c_{n}p_{n})$

$p_n$ ne peut pas réprésenter à la fois le côté de chacun des carrés et la somme $c_{1}p_{1} + c_{2}p_{2}+ ... + c_{n}p_{n})$
Il y a une confusion dans les notations.

Pour le calcul de $C$ _n $P_n$ , c'est juste mais il faut l'organiser un peu plus judicieusement.

$cnpn=13(83)n−1c_np_n=\frac{1}{3}(\frac{8}{3})^{n-1}$

Suite géométrique
Premier terme =C1P1=1/3
Raison qQ=8(1/3)=8/3

Ah d'accord pour l'erreur, ça doit être une erreur dans l'énoncé du coup.
Du coup pour calculer $p_{n}$ il faut faire ce calcul :
$qn+1−1q−1=83n+1−183−1\frac{q^{n+1}-1}{q-1} = \frac{\frac{8}{3}^{n+1}-1}{\frac{8}{3}-1}$ C'est bien ça? Si oui comment on le calcule vu qu'on ne connait pas n?

Ah d'accord pour l'erreur, ça doit être une erreur dans l'énoncé du coup.
Du coup pour calculer $p_{n}$ il faut faire ce calcul :
$qn+1−1q−1=83n+1−183−1\frac{q^{n+1}-1}{q-1} = \frac{\frac{8}{3}^{n+1}-1}{\frac{8}{3}-1}$ C'est bien ça? Si oui comment on le calcule vu qu'on ne connait pas n?

on calcule l'expression en fonction de n ( c'est tout...)

Fait attention : il n'y a pas n+1 termes , il y en a n.
En plus, il manque le premier terme(1/3)
Donc modifie la formule ( et mets 8/3 entre parenthèses ).

Ensuite, n'oublie pas de multiplier par 4

mtschoon
on calcule l'expression en fonction de n ( c'est tout...)
Je comprends pas cette phrase, ça veut dire quoi?

Donc du coup : $pn=4∗(13(83n)−1(83)−1)p_{n} = 4 * \left(\frac{1}{3} \frac{\left(\frac{8}{3}^{n} \right)-1}{\left(\frac{8}{3}\right)-1 }\right)$
C'est bien ça?

Si j'ai bien compris, on aura un résultat avec n dedans?

C'est ça, mais tu peux maintenant simplifier un peu l'expression.

Fait attention à l'écriture : les parenthèses doivent être autour de 8/3 pour qu'on comprenne $8/3)^n$

$pn=4∗(83)n−15p_{n} = 4 * \frac{\left(\frac{8}{3} \right)^{n}-1}{5}$
Est-ce bien ça?

Oui, il me semble, et tu peux l'écrire :

$45[(83)n−1]\frac{4}{5}[(\frac{8}{3})^n-1]$

Ok merci beaucoup!
Par contre, je sais pas du tout répondre aux question suivantes..

Pour la suite (CnPn²), applique que même principe que pour la suite précédente .

Sauf erreur, tu dois trouver :

$cnpn2=8n−1×(13)2n=8n−1×(19)n=19(89)n−1c_np_n^2=8^{n-1}\times (\frac{1}{3})^{2n}=8^{n-1}\times (\frac{1}{9})^{n}=\frac{1}{9}(\frac{8}{9})^{n-1}$

Tu reconnais une suite géométrique.

Oui c'est bien ça, mais je vois pas ce que Pn et Sn représentent sur le dessin.

J'espère que tu as fait la somme pour trouver Sn

Je te mets sur la voie pour l'interprétation graphique :

Pour ce tu appelles "Pn" (ces confusions de notations sont génantes !):

"Pn"=C1(4P1)+C2(4P2)+...+Cn(4Pn)

Pn est le côté de chacun de des carrés, donc 4 Pn est le périmètre de chacun des carrés, donc...

Pour Sn, Pn² est l'aire de chacun des carrés, donc...

Tant pis, j'ai rendu l'exercice Lundi, c'est pas grave pour les dernières questions. En tout cas merci beaucoup!