Rectangle, cercle et équation du second degré.

[TaronSilver]

Bonjour à tous.
Tout d'abord, j'aimerais préciser que j'ai fini le lycée il y a deux ans, mais après deux années sans faire de maths, je me retrouve à galérer pour quasiment n'importe quel exercice, si bête soit-il...

Voici l'exercice; Un rectangle ABCD dont le côté AB est plus petit que le côté BC, d'aire égale à 48cm^2 est inscrit dans un cercle de cinq centimètres de rayon. On place un point E sur le côté CD à x cm de C (x>0) et un point F à px cm de C sur le côté CB. Déterminer les valeurs de p pour lesquelles on peut construire un triangle isocèle AEF de base EF.

Bon, alors après un peu de galère et un peu de zieutage du côté des réponses pour m'inspirer, j'ai trouvé la longueur des deux côtés, respectivement 6 et 8 cm grâce au thérorème de pythagore et à un peu de bidouillage maison.
(Si jamais; a^2+b^2=10^2; ab=48 => a=48/b puis remplacement de a dans mon équation double afin de trouver cette valeur. Pas très clair, mais je peux mieux expliquer si besoin est.)

Le problème, c'est d'aller plus avant. Je me suis fait des petits dessins pour m'aider à réfléchir, mais la seule chose que cela me donne, ce sont des erreurs de logique...

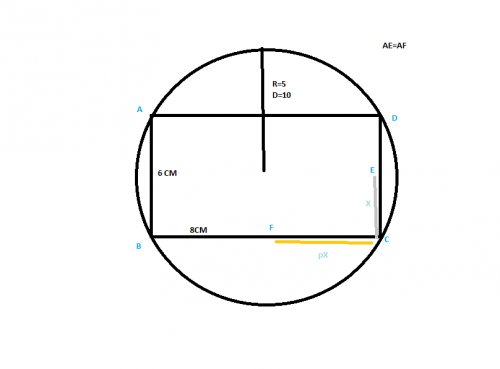
Je m'explique. Partant de l'idée que AF est un vecteur, je me suis dit que je pouvais le calculer comme tel. D'où mes problèmes.

A partir d'içi, j'ai ajouté mon dessin afin de permettre à tout le monde de me suivre.
Si je pars de l'idée des vecteurs; AE=AF, jusque-là
EC=x; FC=px
Mais maintenant, si je suis mon idée;

AE=AD+DE=AD+DC-CE=8+6-x=14-x Pourquoi pas...
AF=AB+BF=AB+BC-CF=6+8-px=14-px ... Voilà. Donc. Evidemment. Ca me semble logique à chaque fois que je l'écris et à chaque fois, je sais qu'il y a une erreur quelque part... p ne PEUT pas avoir une valeur égale à 1...

Par la suite, j'ai essayé en suivant Pythagore.
AF^2=AB^2+BF^2;
AE^2=AD^2+DE^2

Et j'obtiens à nouveau un résultat qui ne veut rien dire.
Et je dois avouer que je sèche, là... Un peu d'aide me serait la bienvenue, merci

[mtschoon]

Bonjour,

Je regarde un peu ton exercice et te donne quelques pistes.

Oui pour AB=6 cm et AD=8 cm.

Ton idée des vecteurs n'est pas bonne. Tu mélanges vecteurs et longueurs.

Ton idée de calcul des distances avec le théorème de Pythagore est la bonne méthode; il faut l'explorer.

Tout d'abord, indique les conditions.

E ∈ [CD] <=> 0 ≤ x ≤ 6
F ∈ [BC] <=>0 ≤ px ≤ 8

AD=8 et DE=6-x . Tu en déduiras l'expression de AE² en fonction de x

AB=6 et BF=8-px . Tu en déduiras l'expression de AF² en fonction de x et p

AE=AF <=>AE²=AF²

Tu utiliseras les expressions trouvées et tu obtiendras une équation du second degré d'inconnue p, x jouant le rôle de paramètre .

Tu t'assureras que cette équation a deux solutions en prouvant que le discriminant est positif

Tu résoudras cette équation et tu obtiendras deux solutions réelles p1 et p2 en fonctions de x

En utilisant les conditions indiquées, tu constateras qu'une seule de ces solutions convient à ton exercice.

Bon travail !