Dm Fonction sinus et autres

[coucou23]

Bonjour à tous, 3 autres personnes de ma classe de terminale S et moi devons faire un DM ensemble, cependant nous le trouvons très compliqué et dès les premières questions nous sommes bloquées, nous avons essayé de continuer en passant les questions où nous bloquons mais cela ne change rien nous n'avançons pas . Je vous mets donc l'énoncé ainsi que ce que nous avons fait en espérant que vous nous donnerez des pistes afin de réussir ce dm.
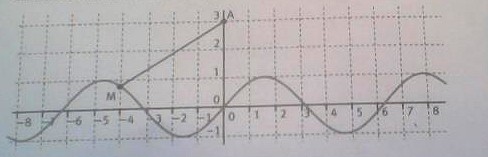
Dans le plan rapporté à un repère orthonormé, on dispose de la courbe C représentative de la foncion sinus et du point A et de coordonnées (0 ; 3 ).
Voir Image
Les objectifs de l'exercie sont de :
_trouver la position de M sur C minimisant la longeur entre le point A et la courbe représentative de la fonction sinus
_déterminer les points M de C en lesquels la tangente à C est perpendicuaire à la droite (AM).

1. Visualiser le problème posé sous Geogebra et conjecturer les résultats.
2. Soit f la fonction définie sur R par f(x) = x - 3 cos x + sin x cos x
   a) Etudier les variations de f sur [(-3π)/2 ; 3π/2], dresser son tableau des variations sur ce même intervalle puis démontrer que l'équation f(x) = 0 admet 3 solutions sur l'intervalle [(-3π)/2 ; 3π/2] dont on donnera un encadrement à 10^-2.
   b) Démontrer que pour tout x appartenant à [3π/2 ; + infini ], f(x) > 0 et que pour tout x appartenant à [- infini ; (-3π)/2 ], f(x) < 0. En déduire que l'équation f(x) = 0 admet 3 solutions réelles.
   c) Etablir le signe de f(x) selon les valeurs du réel x.

a) On note x l'abscisse du point M. Démontrer que la longueur AM s'écrit d(x) = racine carrée de (x² + (sinx-3)²)
b) Démontrer que, pour tout x appartenant à R, d'(x) est du signe de f(x)
c) Etudier les variations de d et conclure quant à la position de M minimisant la longueur entre le point A et la courbe représentative de la fonction sinus.
4.
a) Démontrer que lorsque la longueur AM est minimale, la droite (AM) est perpendiculaire à la tangente à C en M
b) Existe-t-il d'autres points M de C en lesquels la tangente à C est perpendiculaire à la droite (AM) ?
Donc nous avons fait la première question :

1. Il semble que M doit avoir les coordonnées (1,06 ; 0,872) pour que la longueur entre le point A et la courbe représentative de la fonction sinus soit minimale.
   Et il semble que M doit avoir les coordonnées (-3.07 ; -0.072) ou (1,06 ; 0,872) pour que la tangente à C au point M soit perpendiculaire à la droite (AM)
   Ensuite nous avons commencé la question 2 nous avons donc voulu pour étudier les variations de f faire la dérivée de f, ensuite étudier le signe de f' afin d'avoir les variations de f. Mais le problème c'est que nous avons comme dérivée : 1 + 3sinx + cos²x - sin²x et donc nous ne voyons pas comment nous pouvons étudier le signe de f'.
   Nous espérons vraiment obtenir de l'aide, nous ne demandons pas des réponses mais des pistes pour chaque question.
   Merci d'avance.