Suite assez particulière

Bonjour,
J'ai beaucoup de mal avec cet exercice.
Quelqu'un pourrait-il me guider ?

On définit une suite $u_n)$ par $u_0 = 0$ et

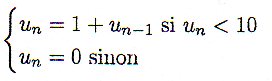
$fichier math$

Calculer $u_{2014}$

Bonjour,

Es-tu sûr de ton énoncé ?

Donne éventuellement le contexte.

Si j'ai bien lu ce que tu as écrit :

Tu as d'abord les premiers termes de la suite arithmétique de premier terme 0 et de raison 1

Uo=0
U1=1
...
U9=9

1+U9=1+9=10

Donc $U_{10}$ vaudrait 0

Je reste perplexe sur la question...

Je suis également très perplexe....

J'arrivais au même résultat que toi, à savoir :

$u_0=0 \ u_1=1+u_0=1+0=1 \ u_2=1+u_1=1+1=2 \ u_3=1+u_2=1+2=3 \ ...... \ u_9=1+u_8=1+8=9$

et à partir du moment où $u_n$ ≥10 alors $u_n=0$

donc $u_{2014}=0$

Mais ça me paraissait vraiment bizarre.
Et ça me parait toujours bizarre.....

Ou alors, $u_{2014}=1$ ??
Car quand $u_n=1+u_{n-1}=1+0=1$

J'comprends pas....

A moins que ça soit un truc du genre :

u10 = 0
u11 = 1+0 = 1
u12 = 1+1 = 2
...
u19 = 9
u20 = 0 --- et on repart pour un cycle à chaque dizaine

Cette dernière interprétation me semble la plus plausible (suite périodique de période 10) et ainsi $U_{2014}$ vaudra 4.

ça me convient mieux également.

Merci