aires fonction

Bonjour, je suis en 1èreS et j'ai un DM de maths et je bloque dessus or je dois le rendre la semaine prochaine. Voilà le problème :

$fichier math$

On avait commencé avec le professeur et il nous à nous demandé de finir. Voilà le début :
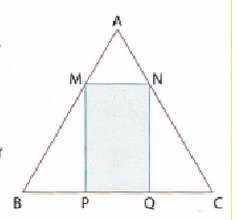
on pose AM = x et x strictement positif, le triangle ABC est équilatéral et de côté a avec a strictement positif.
On appelle H le milieu de [BC], le triangle ABC étant équilatéral alors [AH] est à la fois la médiane, la hauteur et la médiatrice du triangle donc le triangle AHB est un triangle rectangle en H.
D'après le théorème de Pythagore : AB²=AH²+BH² donc AH²=AB²-BH²
=a²-(a÷2)²
=a²-a²÷4
=a²×(1-1÷4)
=a²×3÷4

Donc AH=√(a²×3÷4)
AH=a√3÷2

Or, le triangle ABC étant équilatéral alors ses trois angles sont de même valeur c'est à dire 60°. Le segment [AH] coupe le sommet A par son milieu et coupe aussi le segment [MN] en son milieu. Donc l'angle H vaut 90° et l'angle A vaut 30°, la somme des angles dans un triangle vaut 180° donc l'angle M vaut 60°. L'angle N vaut donc 60° lui aussi. On remarque donc que dans le triangle AMN, les trois angles sont égaux et valent 60° donc le triangle AMN est un triangle équilatéral de côté x puisque l'on avait posé au début de l'exercice AM= x.
Comme AKM est rectangle en K, grâce au théorème de Pythagore on en déduit que : AM²=MK²+KA²
KA²=AM²-MK²
= x²-(x÷2)²
= x²-x²÷4
= x²×(1-1÷4)
= x²×3÷4

Donc AK= √(x²×3÷4)
= x√3÷2
Maintenant que l'on connaît AK on peut calculer KH. KH=AH-AK ce qui donne KH=a√3÷2-x√3÷2

On calcule l'aire du triangle ABC : A(ABC)= (a×AH)÷2 = (a×a√3÷2)÷2= (a²√3÷2)÷2 = a²√3÷4

On calcule l'aire du triangle AMN : A(AMN)=(x×AK)÷2 = (x×x√3÷2)÷2 = x²√3÷4

Voilà où j'en suis, je bloque ici. Je sais qu'après ça il faut que je calcule l'aire des triangles BQM et NPC et à partir de ça trouver une fonction qui devra correspondre à (f)= Aire(ABC)-(Aire(AMN)+Aire(BQM)+Aire(NPC))
En tout cas, c'est ce que notre professeur nous à conseillé de faire mais si vous avez une méthode plus simple alors je ne suis pas contre.
Merci d'avance de bien vouloir m'aider.

merci d'écrire l'énoncé à la main (MP envoyé)
merci de mettre un titre significatif

Bonjour,

Je suppose que H est le projeté de A sur (BC] doncH est le milieu de [BC]
Je suppose que K est le point d'intersection de [MN] avec [AH] doncK est le milieu de [MN]

Le résultats indiqués sont bons.

Pour la suite,

$\text{aire(bqm)=\frac{1}{2}\times bp\times mp$

Pour calculer BP et MP tu peux utiliser le théorème de Thalès appliqué aux triangles BMP et BAH

$\text{\frac{bm}{ba}=\frac{mp}{ah}=\frac{bp}{bh}$

Tu sais que :

$\text{bm=ba-ma=a-x \ ah=\frac{a\sqrt 3}{2} \ bp=\frac{a}{2}$

Tu peux donc trouver MP et BP et en déduire aire(BMP)

Pour aire(NCQ) tu n'as rien à faire vu que aire(NCQ)=aire(BMP)

D'accord, merci beaucoup, je vais essayer et voir ce que ça me donne.
Encore merci !