algorithme-droite

Bonjour, j'ai cet exercice à faire mais je bloque sur les dernières questions..

Jean peut s'installer sur l'un des huits points indiqus sur le cercle.
Le manège comporte un jeu qui consiste à attraper un pompon qui se déplace sur un câble formant un carré dans lequel est inscrit le cercle.
Le manège tourne dans le sens des aiguilles d'une montre, à vitesse constante. Il fait un tour en 24 secondes. Le pompon se déplace dans le même sens à vitesse constante, il fait un tour en 17 sec.
Pour gagner Jean doit obtenir le pompon et il ne peut le faire qu'aux points de contact qui sont notés A,B,C et D sur le dessin. A l'instant t=o, Jean part du point H en même temps que le pompon part du point A.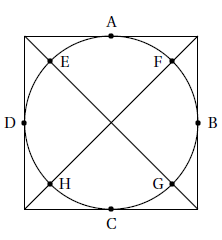

$fichier math$

1: On suppose qu'à un certain instant t, Jean attrape le pompon en A. Jean a déjà pu passer un certain nombre de fois en A sans y trouver le pompon. A l'instant t, on note y le nombre de tours effectués par Jean depuis son premier passage en A et x le nombre de tours effectués par le pompon; x et y sont donc des entiers naturels.
Montrer que (x,y) est solution de l'équation (E) : 17x -24y = 9

]Jean parcourt 3/8 du cercle. Il fait un tour en 24 secondes alors 3/8*24=9 donc il effectue son premier passage en A au bout de 9 secondes. Son deuxième passage à 9+24 sec. soit y le nombre de tours effectués depuis sont premier passage en A, il passera en A toutes les 9+24y sec. Le pompon partant de A il passera en A toutes les 17x sec. J attrapera le pompon quand ils passeront tous en même temps en A donc 17x=9+24y

2:Jean a payé pour 10 minutes. Montrer qu'alors x≤35 et y≤24

10min→600sec donc 17x≤600 ⇔ x≤35 et 9+24y≤600 ⇔y≤24

3:A l'aide d'un logiciel, construire la droite d d'équation : 17x-24y=9 ainsi que les droites d'équation x=35 et y=24. A l'aide du graphique quels semblent être les couples (x,y) d'entiers naturels, avec x≤35 et y≤24 solutions de l'équation (E) ? Vérifier par calculs que les couples trouvés conviennent. Quels inconvénient présente cette méthode?

J'ai construit les droites mais je vois pas que pourrait être les couples (x,y) solutions de l'équation (E)

4:Proposer un algorithme qui permette de trouver tous les ( x : y ) d'entiers naturel , avec x<35 et y<24 solutions de l'équation (E) : 17x-24y=9 .
Écrire le programme associé avec un logiciel au choix . Le tester et vérifier les résultats obtenu au c.

Je ne sais vraiment pas comment m'y prendre pour faire cet algorithme

et enfin : 5: Conclure et indiquer au bout de combien de minutes Jean peut attraper le pompon

J'espère que vous pourrez m'aider. Merci d'avance

Bonjour,

Je regarde seulement les questions 3) et 4) qui te posent problème.

$\leftrightarrow y=\frac{17}{24}x-\frac{3}{8}$

Pour la 3), avec un logiciel, en mode graphique , fait afficher les graduations.

Pour 0≤x≤35,
tu fais tracer la droite d'équation
$y=1724x−38y=\frac{17}{24}x-\frac{3}{8}$

En observant soigneusement le graphique, grâce aux graduations, tu devrais lire les couples (x,y) de naturels satisfaisants.

Sauf erreur, il s'agit de (9,6) et (33,23)

Pour la 4), je te joins un algorithme fait avec Algobox : analyse le pour comprendre la démarche et fais l'algorithme comme tu as l'habitude.

Remarque : floor(y) est la partie entière de y
floor(y)=y est une façon de déterminer si y est entier.

$fichier math$

En faisant fonctionner cet algorithme, tu dois obtenir :

(x,y)=(9,6)
(x,y)=(33,23)

Merci pour cette réponse rapide mais pour la question 3, pourquoi c'est (9,6) et (33,23) et pas d'autres points? Parce qu'il y a pas que ceux là qui sont solutions de l'équation (E) si?

Il s'agit des couples (x,y) d'entiers naturels

C'est peut-être cela qui t'a échappé.

Ce n'est pas la méthode demandée par ton énoncé, mais pour mieux comprendre, tu peux peut-être utiliser ta calculette , avec la fonction Table.

Tu mets Y=(17)/(24)x-3-8
Avec Table, pour toute valeurs x naturelles (0,1,2,3,...,35), tu peux trouver les valeurs correspondantes de y. Tu constateras que les seules valeurs naturelles de y sont obtenues pour x=9 et pour x=33

Ah oui effectivement, merci beaucoup
Quand vous dîtes "fais l'algorithme comme tu as l'habitude", ça veut dire que je prends l'algorithme que vous m'avez présenté et je le modifie c'est bien ça?

Oui, c'est bien ça.

J'ignore tes habitudes relatives à l'algorithmique.

J'ai pris Algobox (logiciel gratuit que tu peux télécharger) car cela permet de taper l'algorithme et de le tester (et éviter ainsi les erreurs)
Si tu connais, tu tapes l'algorithme et tu l'utilises.

Sinon, tu l'écris avec la méthode indiquée par ton professeur ( peut-être langage dit "naturel"...)

A toi de voir