Calcul du volume de sphère et cylindre à l'aide des fonctions

Bonjour

J'ai un problème sur un exercice dont je ne comprends rien !
j'ai mis mes réponses dont je pense fausse ..

figure ;

c'est un cylindre inscrit dans une demi sphère de rayon 6 cm

quand on mets à plat la figure on a :

donc la demi sphère de rayon : 6 cm
et un rectangle ( comme ci-contre):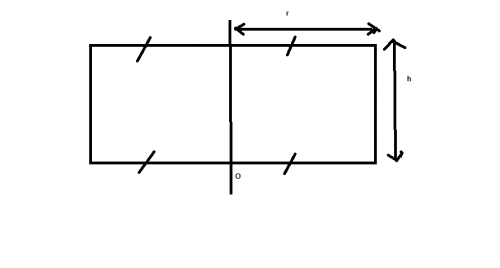

$fichier math$

q1 : dans quel intervalle peut varier la hauteur h du cylindre ?

ma réponse :

elle peut varier suivant la valeur de h

est-ce juste ?

q2 : justifier que r et h sont liées par la relation : r²+h²=36

je n'ai pas répondu : mais je sais qu'il y a un rapport avec l'aire ou je ne sais pas ...

q3) démontrer que le volume du cylindre est donnée en fonction de la hauteur par V(h)=36π $p i$ -π$$pi$h^3$

je n'ai pas trouvé...

q4)a) çà se complique ...

estimer avec le logiciel ou la calcultatrice , la hauteur du cylindre de volume maximal .

quel volume maximal ? comment sur la calculette ?

q4)b) comparer la valeur obtenu pour h à 2√3
on admet que la valeur de h réalisant le maximum est 2√3
calculer le volume maximal du cylindre et de son rayon
.

répnse : je ne sais pas -

q5)

quel pourcentage du volume de la demi sphère , le cylindre de volume maximal occupe t-il ?

voilà :
je suis en galère et j’espère obtenir de l'aide !!

Merci

Bonsoir Delphinne31aka,

La hauteur du cylindre peut varier de 0 à 6 cm vu que la hauteur maximale de la sphère est 6.
Fait une figure et applique la propriété de Pythagore.
Quelle est la formule pour le volume d'un cylindre ?

Bonsoir ,

Merci Noemi de m'avoir répondu !!

Je ne comprend pas votre réponse de la question 1 car on ne connaît pas la hauteur max. de la sphère.

Pour la 2) , j'ai chercher et je ne sais pas sur quel figure ma placer -
J'ai une idée mais bon ...

mon idée : [ on va appellé le rectangle ABCD] sachant que O est le milieu de [DC] .
Je prends le triangle : BCO ?? + après application du théorème de pythagore ?

pour la 3) la formule est : πr²h
Mais je ne comprends toujours pas cette question

Sinon , merci beaucoup !

Bonjour Delphinne31aka,

La demi sphère a son sommet à 6 cm donc c'est la hauteur maximale possible pour le cylindre.
Trace un demi cercle et inscrit un rectangle puis place r, h et 6.

Bonjour ,

Pour la question 1) , je viens de comprendre .

Pour la question 2) , voici le schéma :

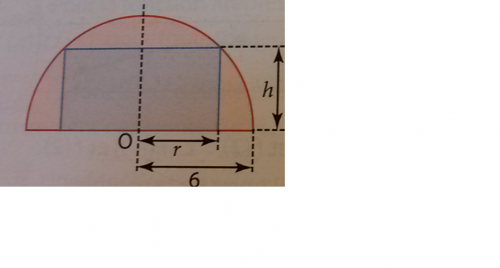
$fichier math$

Et ensuite ?

est-ce que je nomme le rectangle puis me place dans le triangle ou
r et h sont les côtés ?

Mais je ne comprends toujours pas le =36 dans
la relation : h²+r²=36

Trace le triangle OAB,
OA = r et AB = h, et OB = 6
Applique la propriété de Pythagore dans ce triangle.

Donc pour la 2)

Dans le triangle OAB, est rectangle en A , donc
d'après le théorème de Pythagore , on a :
OB²=OA²+AB²
OB²=r²+h²
6²=r²+h²
36=r²+h²

Donc r et h sont liés par la relation du théorème de Pythagore .

C'est bon ?

Pour la question 3 , le volume d'un cylindre est : πr²h

Le volume donné dans l'énoncé est : 36πh-πh³

Je comprends le début : 36πh mais je ne comprends pas : -πh³

Pour la question 3, tu remplaces dans V = πr²h,
r² par 36-h²

je ne comprends toujours pas ...

Tu as trouvé la relation r² + h² = 36,
tu déduis r² = 36 - h² (transformation de formule)

le volume du cylindre V = πr²h
tu remplaces r² par 36 - h²
soit
V = π(36-h²)h
tu développes
V = ...

V=πr²h
Donc V=π(36-h²)h = h36+h*(-h²)π = 36h-h³π

mais ce n'est pas égale à 36πh-πh³ ?

Ou j'ai trouver çà :

π*(36-h²)h
(36π+π(-h²))h
36πh-h³π

Je pense que c'est çà !!!

Pour la question 4 , quel logiciel , ou comment sur une calculette pour connaître la hauteur du cylindre de volume max ?

Pour la q3) : merci beaucoup de m'avoir éclaircit !

A la calculatrice, tu peux :
avec le tableau de valeur faire varier h et chercher le maximum
avec le trace de la courbe, rechercher maximum sur le graphique.

D'accord je vais essayer
Mais je ne comprends pas : faire varier h

merci déjà pour tout ce que vous m'avez aidé !
merci beaucoup !

Tu peux faire varier h de 0,5 en 0,5.

?

A vrai dire , j'ai une nouvelle calculette ( TI-82] dont je ne sais me servir

Tu écris dans Y1 la fonction en remplaçant h par x ;
puis dans la définition de la table tu programmes un pas de 0,5 et tu analyses les résultats dans table.

D'accord ! merci

je trouve 3=254.47 donc c'est le max de tous

donc je conclue : d'après la calculette , 3 est la hauteur du cylindre de volume maximal

C'est çà ?

Pour 4)b) : 2√3=3.45 etc...
Donc pour la comparaison , je dis :
A 0.5 près , ce sont les mêmes nombres.

C'est bon ?

et pour calculer son volume maximal du cylindre ET son rayon : je ne sais pas...

Et 3,5 ?

Puis tu compares 2√3 et 3,5.

Je n'arrive pas à avoir les pas de 0.5

Dans définir table tu inscris 0,5 à pas.

Ah si c'est bon ! je trouve 3.5=261.14

donc je pour la réponse à ma question je dis :

d'après la calculette , 3, 5 est la hauteur du cylindre de volume maximal

t pour la 4)b) : ce sont les mêmes nombres !
car 2√3=3.46... mais arrondi à 0.1 près = 3.5

donc je peux répondre par quelle phrase ?
ce sont les mêmes nombres , ou ils sont égales ?

Précise que 3,5 est la valeur arrondie au dixième de 3,46.

D'accord
merci

ensuite , il me demande de calculer le volume maximal du cylindre et son rayon .

Donc je remplace dans 36πh-h³π , h par 3.5 ?

Tu remplaces h par 2√3

Donc 36πh-h³π =
362√3π-2√3³π=
72√3π-2√3³π

Sauf que 2√3³=10,39230485
et 2√3³*π=32.64838856

Donc je fais quoi ?

Il faut calculer la valeur exacte :
36πh-h³π =
362√3π-(2√3)³π=
72√3π - 24√3π=
....

J'avais pas mis les parenthèses ...

donc c'est égal à 48√3 ?

Il ne faut pas oublier π
48√3π

Ah oui :rolling_eyes:

est ce que : 48√3π répond aussi à la question :
de calculer le volume maximal du cylindre
et son rayon

?

Tu as calculé que le volume, recherche la valeur de r avec la relation
r²+h²=36

r²=36-h²

donc r²=36-(2√3)²
r²=36-2*3
r²=36-6
r²=30

Le rayon est √30

C'est çà ?

Non,

r²=36-h²
r²=36-(2√3)²
r²=36-4*3
r²=36-12
r²=24
r = 2√6

Ah ... je pensais que 2√3 : on enlève la √ donc 2*3

Ah ... je pensais que 2√3 : on enlève la √ donc 2*3

Quand il y a un ²

(2√3)² = 2√3 2√3 = 43

et pour les unités ( pour le volume max.) c'est 48√3π
cm³

et pour le rayon c'est 2√6
cm?