Probabilité le lièvre et la tortue

Bonjour,
Voilà j'ai un exercice et je sèche complétement sur la réalisation de l'algorithme.

Je ne comprends même pas la valeur à donner à P T et L je n'arrive pas du tout à construire l'algorithme. merci de m'aider

pour les questions une et deux pas de problème.

Le lièvre lance le dé (un dé à six faces parfaitement équilibré). . . la tortue, quant à elle, est déjà partie (pas très fair-play ça !). Le temps que le lièvre découvre le numéro sorti (compter une petite quinzaine de se- condes. . . depuis le temps, il n’est plus tout jeune et commence à avoir quelques problèmes de vue), la tor- tue parcourt 1 mètre (elle, par contre, elle est restée en pleine forme !). S’il fait un 6, il saute en une seconde du départ à l’arrivée (distants de 6 mètres) sinon, il patiente sur place.
Le premier qui atteint l’arrivée a gagné.

Déterminer si l’énoncé est cohérent au niveau des vitesses respectives du lièvre et de la tortue.
Si le lièvre fait son premier 6 au cinquième lancer de dé, qui gagne ? Et si c’est au sixième lancer ?
Pour déterminer qui semble avoir le plus de chances de gagner, on décide de simuler plusieurs fois cette course à l’aide d’un algorithme que l’on traduira ensuite en programme pour la calculatrice.

(a) Recopier et compléter l’algorithme suivant :

P prend la valeur 1
Pour T allant de 1 jusqu’à 5
L prend aléatoirement pour valeur un nombre entier de 1 à 6
P prend la valeur P × (L − 6)
FinPour Si . . . Alors
Afficher « . . . a gagné ! »
Sinon
Afficher « . . . a gagné ! »
FinSi

(b) Traduire l’algorithme précédent en programme pour la calculatrice et l’exécuter plusieurs fois.
Qui semble avoir le plus de chance de gagner ?

(c) (facultatif donc toute recherche même incomplète peut-être intéressante et donner un bonus !) En s’inspirant de l’algorithme écrit dans la correction de l’exercice de simulation du jeu PILE ou FACE, proposer un algorithme qui réalise un échantillon de n simulations de course (n choisi au
début de l’algorithme) et qui affiche, pour cet échantillon, la fréquence de gain de la tortue.

Sur un échantillon de taille n = 400, on a trouvé une fréquence de gain de la tortue de 42%. Donner un intervalle qui permet d’estimer, avec un niveau de confiance de 95%, la fréquence théorique (c.a.d. la probabilité) de gain de la tortue à cette course.
Moralité ?

Bonjour,

Je trouve que l'algorithme que tu as écrit est bizarre. Les notations ne sont pas explicitées et la démarche me laisse perplexe...Je ne peux donc pas t'aider à le compléter.

A toute fin utile, je te propose un algorithme fait avec Algobox qui applique l'énoncé que tu as donné :

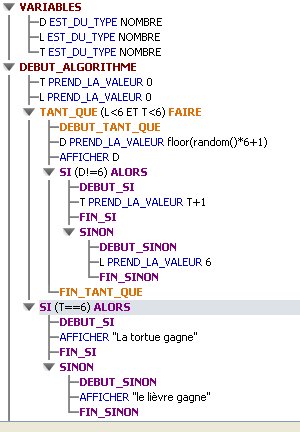
$fichier math$

Notations utilisées :

D est le résultat d'un lancer de dé
L est la distance parcourue par le lièvre ( comptée en mètres)
T est la distance parcourue par la tortue ( comptée en mètres)
La ligne "D PREND LA VALEUR floor(random()*6+1" veut dire, en langage Algobox, que D prend une valeur entière aléatoire comprise entre 1 et 6
La ligne "Si D != 6" veut dire, en langage Algobox,"Si D est différent de 6"

A toi de voir ce que tu peux faire avec...

Merci,
L'algorithme, est préparé par le prof. Nous devons le compléter. J'ajoute que je n'arrive pas à résoudre la question C de l'exercice 3. Je n'arrive pas à trouver la formule sur algobox pour n simulation.

Merci encore

Il n'y a pas de formule particulière pour n simulations.

Tu déclares n comme variable nombre.
Avec "LIRE n", le programme s'arrête et l'utilisateur choisit la valeur de n

Tu déclares i comme variable nombre.
Tu utilises la boucle :

Pour i allant de 1 à n
...
Fin de Pour