équation valeur absolue

Bonjour, j'ai un exercice où il faut résoudre l'équation |2x+3| = 4
J'ai réussi à la résoudre mais après il faut vérifier le résultat graphiquement et ça je ne sais pas comment faire.

Merci de votre aide et au revoir

Bonjour,

Piste,

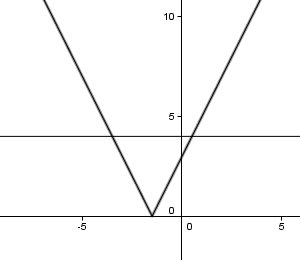
Tu traces la représentation graphique de la fonction f définie par f(x)=|2x+3|(composée de de 2 demi-droites)

Tu traces la représentation graphique de la fonction g définie par g(x)=4

Tu lis les abscisses des deux points d'intersection trouvés.

$fichier math$

Bonjour, Explique déjà comment tu as résolu l'équation et donne les solutions.

Bonjour Mathtous,

Tu as posé une très bonne question à rosepounette !

(Comme je dois quitter le forum, je te laisse poursuivre avec elle)

Bonjour Mtschoon, désolé, messages croisés.
Mais le tien donne la solution demandée, le sujet devrait donc être clos.

Bonjour, alors d'abord on étudie le signe de 2x+3 . On a 2x+3 qui est une fonction affine avec a = 2 > 0 , elle est donc croissante et s'annule en -3/2
On fait le tableau de signe

On revient à l'équation
On fait un tableau de signe avec la valeur -3/2 qui s'annule en 0 , et entre -infini -3/2 on a -(2x+3) = 4 et entre -3/2 et +infini on a 2x+3 = 4

Si x≥-3/2 , il faut résoudre
2x+3=4
2x=1
x= 1/2
Vérification , on a bien 1/2 ∈ ]-3/2; +infini[ , donc 1/2 est bien solution

Si x ≤ -3/2, il faut résoudre
-(2x+3)=4
-2x-3 = 4
-2x = 7
x = -7/2
Vérification, on a bien -7/2 ∈ ]-∞; -3/2[ , donc -7/2 est bien solution

Voila comment j'ai résolue l'équation

Merci beaucoup en tout cas mtschoon , au revoir

Très bien.
Le graphique donné par Mtschoon correspond aux variations de la fonction f(x) = |2x+3| dans chacun des deux intervalles.
Il te suffit alors, comme elle l'a dit, de lire les abscisses des points d'intersection avec la droite d'équation y = 4 puisque c'est ce que l'on souhaite.
Si le graphique est assez précis, tu dois retrouver tes deux solutions.

Oui en effet je peux voir que sur le graphique les deux points d'intersections correspondent à mes deux solutions.

Et merci beaucoup mathous, au revoir

De rien.
A+