Calcul du volume d'une calotte sphérique de hauteur inconnue

Voilà, je dois calculer le volume d'une calotte sphérique dont je connais le rayon de la shère : OA=6,5 cm et le rayon de la calotte IM=6 cm

Comment faire pour calculer la hauteur ? et par conséquent le volume de cette calotte sphérique ?

Bonsoir Amapola62,

As tu fais un schéma ?
Cherche un lien entre OA, IH et h ? Triangle ?

J'ai fait un shéma : AIM est un triangle rectangle h=AI=AO (6,5 cm)+OI (inconnu)
IM = 6 cm
2 droites sont perpendiculaires à AI, une qui passe par O et qui semble correspondre au rayon de la sphère à l'horizontal (soit 6,5 cm) et IM qui mesure 6 cm.
J'ai donc 2 triangles rectangles :
-Un isocèle ayant 2 côtés de 6,5 cm correspondants au rayon de la sphère
-AIM ayant un côté AI de : 6,5 cm + x et un côté IM de 6cm...

En fait on peut construire de multiples triangles dans cette figure :

AOG = Triangle rectangle isocèle de 6,5 cm de côté
AGI = triangle quelconque de base AI = 6,5 + x et de hauteur OG = 6,5 cm
AIM = Triangle rectangle ayant un côté AI de : 6,5 cm + x et un côté IM de 6cm
OGI = Triangle rectangle ayant un côté OG de 6,5 cm et un côté OI de x cm
OMI = Reflet en miroir et plus petit du précédent ayant un côté IM de 6 cm et un côté OI de x cm

Je ne sais pas vraiment à quel théorème me référer dans un cas comme celui-là...

La calotte à une hauteur supérieure au rayon h = AO + OI ??

Oui c'est cela...

La hauteur de la calotte (h) est supérieure au rayon. La hauteur de la calotte correspond au segment [AI], qui se compose du segment [AO] qui est le rayon de la sphère, et du segment [OI] dont on ne connait pas la mesure.

La hauteur mesure donc : 6,5 cms + x

Bonjour,

Une piste pour avancer en attendant que Noemi soit de retour :

Est-cela ? (figure en coupe)

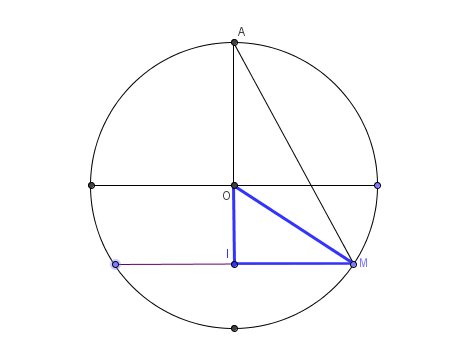
$fichier math$

Si c'est ça, tu peux appliquer le théorème de Pythagore dans le triangle OIM pour trouver IO² puis OI.

Tu tires les conséquences.

Oui c'est cela ...mais je ne connais pas la longueur OM...seulement la longueur IM et la longueur AO...

Puis-je vraiment appliquer le théorème de Pythagore dans ce cas ?

Je sais que dans le théorème de Pythagore le carré de l'hypothénuse et égal à la somme des carré des deux autres côtés...

Mais je n'ai pas la longueur de l'hypothènuse...

Je viens de réaliser que OM est un rayon de la sphère...reste à le prouver avec la bonne propriété...

Oui

OM est le rayon de la sphère.

L'hypothénuse du triangle rectangle concerné (en bleu sur le schéma) est OM : OM=OA=6,5 m .

Alors, applique tout simplement la formule de Pythagore OM²=...

C'est bon, j'ai résolu l'exercice ^^ Merci pour votre aide.

De rien ! nous avons fait au mieux.