Calculer la dérivée d'une fonction et étudier ses variations

[learhte]

Bonjour , je ne comprend pas ce problème merci de bien vouloir m'aider

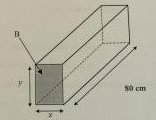
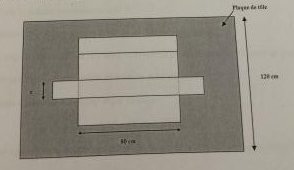
l'objectif principal est de connaître la contenance maximum du réservoir. Pour avoir le moins de pertes possibles dans la découpe, il est décidé d'utiliser 1.20m de largeur de tôle. Pour cela le périmètre de la base B du réservoir doit être égal à 120cm

1. Déterminer la hauteur y du réservoir en fonction de la largeur de x .
2. Déterminer le volume V du réservoir en fonction de x .
3. Soit la fonction f définie sur l'intervalle [0.60] par : f(x)= -80x²+4800x
   a- calculer la dérivée de f'
   b- étudier le signe de f' (x) sur l'intervalle [0.60]
   c- en déduire la valeur pour laquelle la fonction f admet un maximum.
   e- calculer ce maximum.
   f- représenter graphiquement la fonction f
4. Quelle est donc la largeur x du réservoir pour avoir un volume maximum.
5. Quel est le volume maximum en cm3
6. En déduire la contenance maximum de ce réservoir en litres.
7. Il est maintenant décidé de fabriquer un réservoir pouvant contenir 70 litres de gasoil.
   a- établir une équation permettant de traduire cette contrainte.
   b- Résoudre l'équation du second degrés suivante: 80x²-4800x+70000=0
   c- Quelles sont les deux largeurs possibles du réservoir pour avoir une capacité de 70 litres.
   d- En déduire les hauteurs correspondantes.

Merci beaucoup d'avoir répondu à mon message

• ici, on peut mettre les images, non le texte scanné, d'où la modification effectuée.*

[mtschoon]

Bonjour,

Piste pour démarrer,

Le périmètre de la base vaut : 2x+2y=120

D'où : x+y=60 <=> y=60-x

Le volume du réservoir vaut : (x fois y) fois 80

En remplaçant y par son expression en fonction de x :

$V(x)=x\times (60-x)\times 80=(60x-x^2)\times 80=4800x-80x^2$

La fonction f à étudier est donc V

Essaie de poursuivre.