3. Calculs d'angles et distances dans un triangle à l'aide des fonctions trigonométriques

Calculs d'angles et distances dans un triangle à l'aide des fonctions trigonométriques

  • D

    Bonjour ,

    je bloque sur un exercice de trigonométrie …. merci de m'aider

    ABC est un triangle dont les trois angles: BAC , ABC et BCA sont aigus.
    On a tracé sa hauteur [AH] issue de A ( on note AH=h )
    AB=c
    BC=a
    CA=b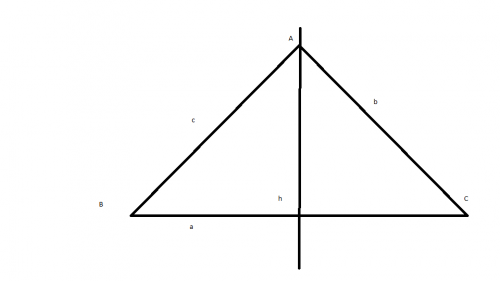

    fichier math

    1. exprimer sinB et sinC à l'aide des longueurs apparaissant sur la figure
    2. exprimer l'aire du triangle ABC à l'aide des longueurs apparaissant sur la figure
    3. En déduire 2 expréssions de l'aire du triangle ABC , faisant intervenir sinB et sinC
    4. Démontrer que b/sinB = c/sinC

    Mes réponses :

    1. -Dans le triangle ABH , rectangle en H :
      sinB=AH/AB
      sinB=h/c
      -Dans le triangle ACH , rectangle en H :
      sinC=AH/AC
      sinC=h/HC
    2. Aire de ABH=ha/2
      Aire de ACH=h      HC/2
      Donc l'aire de ABC=h+a/2+h*HC/2 = 2hHC+a/4
    3. je n'ai pas trouvé
    4. je n'ai pas trouvé

    Merci de m'aider et de me dire si j'ai déjà des fautes dans ce que j'ai fais , et de m'aider à répondre
    au deux dernières questions ….

    Merci ^^

    N 1 réponse
  • N
    Modérateurs

    Bonsoir Delphinne31aKa

    1. sinC=AH/AC
      sinC=h/a
    2. Aire de ABC=h*a/2

    Isole h des relations trouvées à la question1 que tu remplaces dans l'expression de l'aire.

    D 1 réponse
  • D

    Donc la réponse de la 2) est h*a/2 ?

    D 1 réponse
  • D

    1. En déduire 2 expréssions de l'aire du triangle ABC , faisant intervenir sinB et sinC
    2. Démontrer que b/sinB = c/sinC
    N 1 réponse
  • N
    Modérateurs

    Tu as trouvé sinB = h/c cela donne h = c sinB
    de même avec sin C = h/b cela donne h = b sinC

    Comme l'aire de ABC = h*a/2
    3) avec h = c sin B; l'aire = c sinB * a / 2
    avec h =b sin C ; l'aire = b sin C *a/2

    1. Ecris l'égalité pour l'aire et simplifie l'expression
    D 1 réponse
  • D

    Pour la réponse 3
    je trouve : sinBBCBA/2 et sinCBCAC/2

    Pour la 4

    je ne sais toujours pas.....

    D 1 réponse
  • D

    pour la 4) j'ai trouvé :
    La hauteur du triangle est de csinB ou bsinC , pour former un 3eme triangle rectangle on peut voir que asinB=bsinA donc a/sinA=b/sinB=c/sinC

    N 1 réponse
  • N
    Modérateurs

    Pour la question 3, j'ai écris la réponse :
    Comme l'aire de ABC = h*a/2
    3) avec h = c sin B; l'aire = c sinB * a / 2
    avec h =b sin C ; l'aire = b sin C *a/2

    1. l'égalité pour l'aire donne
      c sinB*a/2 = b sinC * a/2

    simplifie cette égalité
    ....

Se connecter pour répondre