Equations cartésiennes de droites

Comment choisir le réel k pour que les droites d'équation x = k n'aient aucun point commun avec l'intérieur du triangle ABC ?
Donner l'ensemble des solutions sous la forme d'une réunion d'intervalles.

On a le point A (-2; 7) et les vecteurs u (-2; 4) et v (3; -5).
D1 passant par A de vecteur directeur u et D2 passant par A et de vecteur directeur v
D3 : y + 3 = 0
B point d'intersection de D1 et D3 et C point d'intersection D2 et D3.

J'ai calculé les équations cartésiennes de D1, D2 ainsi que les coordonnées de B et C.
Je suis bloquée à ce stade.
Aidez moi à continuer svp.

BONJOUR ! (un "Bonjour" fait plaisir à la personne qui répond)

Pour pouvoir répondre à la fin de ton exercice, il faut savoir ce que tu as trouvé pour les équations de droites et les coordonnées de B et C, vu que la fin en dépend.

Merci d'indiquer tes résultats.

J'ai trouvé :
d1 : -4x + 2y -22
d2 : -5x -3y +11
B (-7 ; -3) et C (4 ; -3)

N'oublie pas le membre de droite de chaque équation.

Pour d2 :-5x -3y +11=0 est juste.

Les coordonnées du point C(4,-3) aussi.

Par contre, l'équation de (d1) et l'abscisse de B ne correspondent pas à u (-2; 4)

L'équation de (d1) que tu donnes**-4x + 2y -22=0** et le point**B(-7,-3)**correspond à u(-2,-4)

Donc, vérifie ton énoncé écrit et/ou recompte.

Pour le cas où l'erreur serait une faute de frappe dans l'énoncé et les points A, B, C que tu donnes exacts , je te joins un schéma

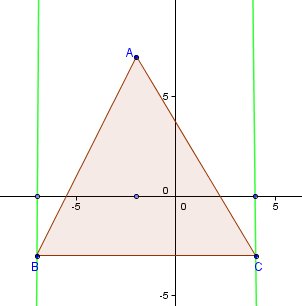
$fichier math$

J'ai tracé en vert les droites d'équations x=-7 et x=4

Tu dois trouver facilement les valeurs à donner à k pour que les droites d'équation x=k n'aient aucun point commun avec l'intérieur du triangle ABC (teinté)

C'était juste une faute de frappe dans l'énoncé, le vecteur u est en fait (-2 ; -4).
Merci beaucoup pour votre aide. J'ai bien compris comment il fallait faire désormais.

C'est bien !