DM maths: vecteurs triangle ABC

Bonsoir, je ne comprend pas l'exercice 4 de mon dm :

la question A est : $→AP\rightarrow AP$
= 2/3 de $→AB\rightarrow AB$

Comment on calcule ça ? Sachant qu'il faut placer P .

Merci !

Bonjour,

$AP⃗=23AB⃗\vec{AP}=\frac{2}{3}\vec{AB}$

Tu partages le segment [AB] en 3 parties égales.
Tu places P au 2/3 du segment en partant de A ( c'est à dire à 1/3 en partant de B)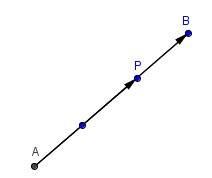

$fichier math$

Merci, ça m'a aider à placer les premiers points sauf pour le point R , on me dit que le vecteur BR= -1/3 du vecteur BC . Je pense que c'est le - qui me dérange j'ai placer les points dans le triangle en pièces jointes.

Pour le 2° , comment on lit les coordonnées les points sur un repère quelconque, ? on me demande de donner les coordonnees des pts A B et dans le repère ( A, ⇒AB, ⇒AC)

Merci de votre aide ! triangle

R est mal placé sur ton schéma car tu as pris : $BR⃗=13BC⃗\vec{BR}=\frac{1}{3}\vec{BC}$

Vu que -1/3 est négatif, $BR⃗\vec{BR}$ doit être de sens contraire à $BC⃗\vec{BC}$

(Tu dois trouver les points P,Q,R alignés sur ton schéma)

Pour ta seconde question,
A est l'origine du repère donc :
A a pour coordonnées (0,0)

$AB⃗\vec{AB}$ est de vecteur unitaire de l'axe des abscisses donc :
B a pour coordonnées (1,0)

$AC⃗\vec{AC}$ est de vecteur unitaire de l'axe des ordonnées donc :
C a pour coordonnées (0,1)

Merci !

Je suis désolée mais je ne comprends vraiment pas le 3°) aussi : on me demande de Prouver que ⇒AR = 4/3 ⇒AB - 1/3 ⇒AC puis de donner les coordonnees des pts P,Q et R

Je n'arrive pas du tout !

Merci de votre aide

J'ai l'impression que tu maîtrises mal ton cours.
Je te conseille de l'approfondir.

Relation de Chasles ;

$AR⃗=AB⃗+BR⃗\vec{AR}=\vec{AB}+\vec{BR}$

$BR⃗=−13BC⃗=−13(BA⃗+AC⃗)=−13BA⃗−13AC⃗=13AB⃗−13AC⃗\vec{BR}=-\frac{1}{3}\vec{BC}=-\frac{1}{3}(\vec{BA}+\vec{AC})=-\frac{1}{3}\vec{BA}-\frac{1}{3}\vec{AC}=\frac{1}{3}\vec{AB}-\frac{1}{3}\vec{AC}$

En remplaçant dans la première formule écrite, tu dois trouver l'expression souhaitée.

R a donc pour coordonnées (4/3, -1/3)

Essaie de trouver les coordonnées de P et Q (il n'y a aucun calcul à faire)

Je me doutais bien que c'était la relation de chasles mais je ne comprend toujours pas !! Que faut il remplacer

Désolé de vous faire reprendre une deuxième fois !

Merci de votre aide

$AR⃗=AB⃗+BR⃗=AB⃗+13AB⃗−13AC⃗=....\vec{AR}=\vec{AB}+\vec{BR}=\vec{AB}+\frac{1}{3}\vec{AB}-\frac{1}{3}\vec{AC}=....$

Pour P et Q, j'espère que tu n'auras pas de difficulté pour trouver P(2/3,0) et Q(0,1/3)
Pour cela, il te suffit de regarder les constructions faites (ou les égalités vectorielles données par l'énoncé)