Etudier la fonction aire d'un triangle

Bonsoir, j'ai un petit exercice illustré sur feuille que je n'arrive pas à faire. Si vous pouvbiez m'aider ce serait gentil :

Dans un quart de disque, un point M est mobile sur un segment [AB]. N est le point de l'arc de cercle de BC ( C vient du segment AC ( je le précise car vous n'avez pas l'image devant vous)) tel que le triangle AMN soit rectangle en M.
On s'intéresse à l'aire du triangle AMN lorsque M décrit [AB].
On prend AB comme unité de longueur (AB=1)

On pose AM = x. Soit f la fonction qui à x associe l'aire du triangle AMN.

Dans quel intervalle, la variable x peut-elle prendre ses valeurs ?
Exprimer en fonction de x la distance MN.
Retrouver alors l'expression de f(x) = x/2 racine carrée de 1 -x²
Montrer que pour tout x, (f(x))² -(1/4)² = -1/16 (2x²-1)²
En déduire que pour tout x, f(x) est inférieur ou égal à (1/4)
Calculer f(racine carré de 2 / 2) et conclure.

Merci d'avance,

L'intervalle [0;1]
Théorème de Pythagore : 1-x² = MN²
Pour celui-ci je ne sais pas si il faut remplacer x par 1. Merci d'avance pour vos réponses.

Et le reste je n'ai pas compris comment faire ^^

Bonsoir,

Ce serait bien de mettre le graphique (seulement le graphique).

Pour cela, clique sur "Ajoute une image" en dessous du cadre texte et suis les indications.

Est-ce cela la figure ?

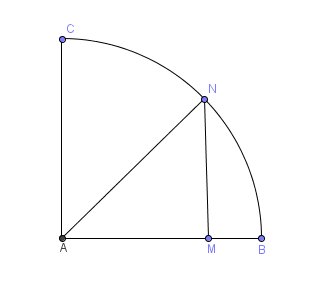
$fichier math$

Si c'est cela, je regarde tes réponses.

Oui pour 1) et pour 2)

AM=x

$f(x)=aire(AMN)=AM×MN2=x×1−x22f(x)=aire(AMN)=\frac{AM \times MN}{2}=\frac{x\times \sqrt{1-x^2}}{2}$

pour la 4 du coup je développe mais j'vois pas comment merci énormément de ton aide ! oui pour la figure

Tu n'as pas répondu à ma question...j'espère donc que le graphique que je t'ai proposé est le bon ( mais une autre fois, il faudra le faire).

Prends le temps de réfléchir.

$\text{(f(x))^2-(\frac{1}{4})^2=\frac{x^2(1-x^2)}{4}-\frac{1}{16}$

Tu réduis au même dénominateur 16 et tu transformes le numérateur.

Hmmm.. après réfléxion cela fait

4x²(4-4x²) / 16 - 1/16

Donc, 4x²(4-4x²)-1 / 16

Désolé si c'est pas ça mais j'suis pas très fort en maths

(Sinon pour le graphique je l'avais fait mais je pensais qu'il était interdit de poster des images)

non, car tu as multiplié deux fois par 4

$\text{(f(x))^2-(\frac{1}{4})^2=\frac{4x^2(1-x^2)-1}{16}=\frac{4x^2-4x^4-1}{16}$

Maintenant, tu mets -1/16 en facteur.

En ce qui concerne les images, je le joins quelques consignes :
Citation
Dans quels cas les scans sont-ils autorisés dans le forum ?
Pour des raisons de droits, l'affichage de scans de documents n'est pas autorisé dans le forum, sauf pour des figures ou des tableaux indispensables à la compréhension de l'exercice. Les liens vers des pages internet contenant le sujet scanné sont également interdits.

comment ca ?! ( dsl j'suis très nul en maths )

$\text{\frac{4x^2-4x^4-1}{16}=-\frac{1}{16}(.....................)$

Essaie de réfléchir à ce qu'il faut mettre à la place des pointillés.

4x²-4x(puissance 4) ?

Non.

Pense au signe "-" qui est en facteur et n'oublie pas le "1" que tu sembles avoir perdu.

-4x²-4x(puissance 4)-1 ?

Il y a encore des erreurs dans les signes. Regarde de près.

-4x²-4x(puissance 4)+1

on fini ca rapidement en faisant le 5) et 6) comme ça j'pars me coucher

Citation
on fini ca rapidement en faisant le 5) et 6)

? ? ? ! ! !

Avant la 5) et la 6), il faut queTU commences à faire la 4) correctement.

Pour ta dernière réponse : tu as supprimé une erreur de signes, mais il en reste une.

Continue de regarder de près les signes.

Ce n'est pas difficile .

A cause du "moins" qui est mis en facteur, tu dois changer TOUS les signes de $4x^2-4x^4-1$

Remarque : si ça t'arrange, je te mets le plan de travailpour la fin:

Lorsque tu auras démontré que $(f(x))2−(14)2=−116(2x2−1)2(f(x))^2-(\frac{1}{4})^2=-\frac{1}{16}(2x^2-1)^2$ ,
tu pourras déduire que $(f(x))2−(14)2≤0(f(x))^2-(\frac{1}{4})^2\le 0$
donc $(f(x))2≤(14)2(f(x))^2\le (\frac{1}{4})^2$
donc $\le \frac{1}{4}$
Vu que $f(22)=14f(\frac{\sqrt 2}{2})=\frac{1}{4}$ , l'aire maximale du triangle AMN sera obtenue pour $x=22x=\frac{\sqrt 2}{2}$

Bon travail !

merci énormément ! j'ai fais la même chose avant de voir ce message, ca confirme mes calculs

De rien !

A+