Dérivation et équation de la tangente d'une courbe
-
Aallthekpop dernière édition par Hind
Bonjour, je suis actuellement sur un problème sur les dérivations.
Pour plus de précision, voici l'énoncé :
Dans un hôpital, deux parties sont à des niveaux différents, le dénivelé étant de 50cm pour une distance de 10m. On désire créer une rampe d'accès pour personnes handicapées reliant les deux plates-formes.
On écarte la solution la plus simple qui serait de relier les deux inveaux par un plan incliné rectiligne. En effet, cette solution est rejetée car les raccordements aux extrémités sont jugés trop brutaux et peuvent engendrer des difficiltés pour le transport des matériels et des patients.Un bureau d'études est chargé de trouver une solution dont le profil sera donné par la courbe d'une fonction.
On choisit le reprère othonormé dans lequel A et B ont pour coordonnées respectives (0;0) et (10;0,5).
La courbe doit respecter les contraites suivantes :-elle doit passer par les points A et B
-les tangentes à la courbe en ces points doivent être horizontales.1. a. Soit f une fonction définie de dérivable sur [O;10]. On note f' sa dérivée.
Traduire les contraires que doit respecter la courbe de f à l'aide f et de f'.J'ai mis que tout d'abord, la courbe devait passer par les points A et B.
Qu'en lisant la courbe, on trouve f(0)=0 et f(10)=0,5
Puis que les dérivés en les points A et B soient égales à 0.
Donc que f'(0)=0 et que f'(10)=0.b. Déterminer les réels a, b, c et d tels que la courbe de f définie par
f(x) = ax^3+bc^2+cx+d
sur [O;10] respecte les contraintes.Comme nous n'avons jamais traité la résolution d'équations pour un polynome du troisième degré en classe, je ne sais pas si cela sera juste de la résoudre comme on le fait avec des polynome du second degré.
(Il y a d'autres questions qui suivent mais celle-ci m'empêche d'y répondre.)
Merci de bien vouloir m'aider...

-
Mmathtous dernière édition par
Bonjour,
Exprime f'(x) à partir de f(x).
-
Aallthekpop dernière édition par
Voici mes résultats :
f(x)=ax^3+bx^2+cx+d
donc
f'(x)=3a^2+2x+c(et donc par exemple, si
f'(10) = 0 alors
300a+20b+10 = 0 )
-
Mmathtous dernière édition par
Il y a une erreur :
f '(10) = 0 donne 300a + 20b + c = 0Fais de même pour f(0), f '(0), f(10), tu devrais trouver d=c=0, et il te restera deux équations pour trouver a et b.
-
Aallthekpop dernière édition par
Comme f(0) = 0, alors,
0a+0b+0c+d = 0
Comme f'(0) = 0
0a+0b+c = 0
Comme f(10) = 0,5
1000a+100b+10c+d=0,5
Comme f'(10) = 0
300a+20b+c=0
d = 0 car,
0a+0b+0c+d = 0
0a+0b+0c=-d
-0a-0b-0c=d
0=dc = 0 car,
tout d'abord, c correspond à l'origine du repère, de plus,
0a+0b+c=0
0a+0b=-c
-0a-0b=c
0=cdonc c=d=0.
est-ce bien cela?
-
Mmathtous dernière édition par
Pour d, c'est correct mais un peu lourd.
f(0) = 0 donne :
0a + 0b + 0c + d = 0
D'où d = 0 (c'est suffisant).Pour c, je ne comprends pas
Citation
tout d'abord, c correspond à l'origine du repèreEt précise quelle condition tu utilises : ici, c'est f '(0) = 0.Il te reste 1000a+100b+10c+d=0,5 et 300a+20b+c=0 dans lesquelles tu peux déjà remplacer c et d par 0.
Ça te donne un système de deux équations à deux inconnues : a et b.
-
Aallthekpop dernière édition par
Pour "c", je me suis placée dans le cas f(0) = 0, et donc comme c correspond à l'image pour f(0), j'en ai déduis que c = 0.
Voici mon équation, cependant mes résultat sont étranges :
1000a+100b+10c+d=0,5
300a+20b+c=0comme d=c=0, alors
1000a+100b=0,5
300a+20b=0(je transporte tout pour le premier membre, afin de ne trouver que b)
b=0,05-1000a
300a+20b=0donc je remplace b dans l'autre membre et je trouve
1000a+100b=0
300a+20(0,05-1000a)=01000a+100b=0
300a+0,1-200000a=0⇔0,1-19700a=0⇔a=(0,1/19700)est-ce juste pour le moment avant de continuer? car ce résultat me paraît bizarre et sur mon logiciel geogebra, l'équation finale comporte une "erreur" et la courbe ne se trace pas...
merci
-
Mmathtous dernière édition par
Citation
Pour "c", je me suis placée dans le cas f(0) = 0, et donc comme c correspond à l'image pour f(0), j'en ai déduis que c = 0.Non : f(0) = d.
C'est f '(0) qui fournit c = 0.Citation
1000a+100b=0,5
300a+20b=0Oui, mais quand tu isoles b, ce n'est pas b = 0,05-1000a
Mais c'est 100b = 0,5 - 1000a
D'où b = 0,005 - 10a
Continue : tu devrais obtenir a = - 0,001
-
Aallthekpop dernière édition par
Merci, j'avais oubliée de distribuer ce quotient !
Du coup, cela me donne :
1000a+100b=0,5
300a+20(0,005-10a)=01000a+100b=0,5
300a+0,1-200a = 0 ⇔ 100a+0,1=0 ⇔ 100a=-0,1 ⇔ a=-0,0011000(-0,001)+100b=0,5
a = -0,001-1+100b=0,5
a = -0,001
100b = 1,5
b = 0,015
est-ce bien cela ?
-
Mmathtous dernière édition par
Oui.
-
Aallthekpop dernière édition par
"Pour la suite la fonction f sera obtenue à la question 1.b et sa courbe notée C. Dans un repère orthonormé, la pente d'une courbe en un point est égale au coefficient directeur de la tangente en ce point"
La prochaine question me demande de trouver :
la pente maximale de C, puis de déterminer les coordonnées du point K où ce maximum est atteint, et de dire ce que représente K pour les points A et B.J'en ai déduis que l'on pouvait se servir de la forme dérivée de la fonction f et résoudre une équation
f(x) ax³+bx²+cx+d qui donne f'(x) =3a²+2x+x ?
-
Mmathtous dernière édition par
Il s'agit bien de la fonction précédente ?
Alors remplace a et b par leurs valeurs.
En outre, tu as oublié b dans la formule de la dérivée, et mal dérivé cx.
Mais ici, c et d sont nuls.
-
Aallthekpop dernière édition par
Oui il s'agit bien de la fonction précédente !
(Je parlais de "résoudre une équation" pour trouver les coordonnées par la suite)
Oui, alors cela fait au final :
f''(x)=3a²+2b+0c
lorsque je remplace a et b, je retrouve :
f''(x)=3*(-0,001)²+2*(0,015)+0
f''(x)=0,030003
et donc la pente aura atteint son maximum en K pour f'(x)=0,030003
-
Aallthekpop dernière édition par
Pour trouver les coordonnées du point K, je propose de remplacer l'équation de la tangente de la forme :
y=f'(a)(x-a)+f(a)
par f'(x) et f(x).
Ensuite pour trouver "x" je remplace le réel "y" par 0, et inversement, est-ce bien cela?
-
Mmathtous dernière édition par
Citation
f''(x)=3a²+2b+0cPas du tout. Tu confonds à nouveau x et a.
f '(x) = 3ax² +2bx
Tu remplaces a et b par leurs valeurs, ce qui donne f '(x) = -0,003.x²+ 0,03.x
Tu dois alors chercher le maximum de cette fonction dans l'intervalle considéré.
-
Aallthekpop dernière édition par
Je ne sais pas comment faire.
Il faut que je trouve la/les valeur maximale où f'(x) s'annule sur la domaine de définition considéré, mais je n'y arrive pas...
J'ai factorisée, mais rien ne me saute aux yeux...
f'(x) = -0,03(0,1x²+x)
-
Mmathtous dernière édition par
Il ne s'agit pas de chercher les valeurs d'annulation de f '(x), qui d'ailleurs sont évidentes (0 et 10) et qui correspondent à ce qui est demandé au début.
Il s'agit de chercher le maximum de f '(x) qui est ici un polynôme du second degré.
Étudie les variations de f '(x) et tu trouvera pour quelle valeur de x le maximum est atteint ainsi que la valeur de ce maximum.
Tu sais quand même bien étudier les variations d'une fonction du second degré ?
-
Aallthekpop dernière édition par
Je n'ai pas encore étudier ce chapitre en classe, si il s'agit d'étuder les variations d'unefonction dérivée, car j'ai pour l'instant fait qu'une première partie du chapitre de dérivation, où l'étude des variations n'est pas inclus.
Je n'ai donc aucune idée de comment m'y prendre.
-
Mmathtous dernière édition par
Il s'agit d'une fonction du second degré, vue en classe de seconde!
g(x) = ax² + bx + c est :
d'abord décroissante jusqu'à la valeur ... si a est positif, puis croissante.
Le contraire si a est négatif.
Attention : les lettres a,b,c n'ont rien à voir avec celles de ton problème.
Celles de ton problème sont maintenant inutiles puisqu'on les a calculées.
-
Aallthekpop dernière édition par
Du coup je compte le "c" dans l'expression de la fonction ? (c = 0)
-
Mmathtous dernière édition par
Pas besoin s'il est nul.
Ici, g(x) = -0,003x² + 0,03x
Le coefficient de x² est négatif : la fonction commence-t-elle par croître ou par décroître ? Et jusqu'où ?
Il faut revoir ce que tu as fait en seconde (et ne pas l'oublier).
-
Aallthekpop dernière édition par
Ah autant pour moi, je n'avais pas compris ce que vous vouliez que je fasse ! Oui, je l'ai étudiée en classe de seconde, donc :
Tout d'abord la courbe est tournée vers le haut car a est négatif. (Donc ax²+bx+c ≤0. )
Calcul du discriminant :
Delta = b²-4ac = (0,03)²-(4)(-0,003)(0) = 0,0009
Delta > 0, donc ax²+bx+c = 0 admet deux solutions :
x1 = (-b-√d/2a) = -(0,03)-√0,0009/2*(-0,003) = 10
x2 = (-b+√d/2a) = -(0,03)+√0,0009/2*(-0,003 = 0
et le sommet de la courbe a pour point d'abscisse :
-b/2a = 5
donc
ax²+bx+c ≤ 0 sur ]-∞;0] ∪ [5;+∞[ et ax²+bx+c≥0 sur [0;10]
-
Aallthekpop dernière édition par
La courbe commence à croître jusqu'à 5, puis décroît jusqu'à 10.
-
Mmathtous dernière édition par
Citation
Donc ax²+bx+c ≤0Non : ça dépend des valeurs de x.
Citation
Delta = b²-4ac = (0,03)²-(4)(-0,003)(0) = 0,0009Delta > 0, donc ax²+bx+c = 0 admet deux solutions :
x1 = (-b-√d/2a) = -(0,03)-√0,0009/2*(-0,003) = 10
x2 = (-b+√d/2a) = -(0,03)+√0,0009/2*(-0,003 = 0Pas besoin. Ici, il faut savoir de quelle courbe on parle. Si j'ai utilisé la notation g(x), c'est pour que tu ne sois pas troublé avec les dérivées.
Mais il faut revenir au problème posé : g(x) est en fait f '(x).
Elle s'annule pour x = 0 et x = 10 : on le savait : la tangente à la courbe (celle de f) est horizontale pour ces valeurs.
Le point d'abscisse 5 que tu as trouvé réalise la plus forte valeur de f '(x) dans l'intervalle considéré, c'est-à-dire là où la pente est le plus forte.
Il te reste à calculer la valeur correspondante de l'ordonnée de ce point K et de dire ce qu'il représente pour A et B.
-
Aallthekpop dernière édition par
D'accord, calculons l'image de 5.
f'(x) = -0,003x²+0,03x
f'(5) = -0,003*(5)²+0,03*5
f'(5) = 0,075Les coordonnées du point K sont donc : (5;0,075)
Selon moi, le point K représente par rapport aux points A et B la moitié du parcours effectué. (La moitié de la distance entre ces deux points.)
Voici l'image de cette pente pour plus de précisions :
-
Aallthekpop dernière édition par
Je me suis trompée, je me suis servis de la mauvaise fonction donc je recommence :
f(x) = -0,001x^3+0,015x^2
f(5) = 0,25Coordonnées de K = (5;0,25)
-
Mmathtous dernière édition par
Oui, mais personne ne t'empêche de préciser ce que signifie la valeur 0,75 (trouvée par erreur comme l'ordonnée de K) .
K est en effet situé à mi-parcours, mais ne peux-tu être plus précis ? (regarde ses coordonnées).
-
Aallthekpop dernière édition par
Je pense que 0,75 est l'ordonnée où la tangente à la courbe de point d'abscisse 5 se trouve ?
Je pense plutôt que l'ont devrait le mettre sous cette forme :
0,25 = 25. (25m)
5 correspond à à 5m d'abscisse et donc la moitié de la longeur de la pente, de la distance entre les deux points. Et 25 correpsond à 25 m d'ordonnée et donc la moitié de la hauteur de la pente, ou encore de la distance entre le sol et la pente.
-
Mmathtous dernière édition par
Attention à tes unités : 25 m ?
0,75 n'est pas l'ordonnée du point K puisque l'ordonnée de K (que tu as trouvée) vaut 0,25.
0,75 est la pente maximum, là où la montée est la plus raide.
Mais tu ne réponds pas de façon satisfaisante à la question sur K.
Quelles sont les coordonnées du milieu de [AB] (tu connais celles de A et celles de B).
Réponds rapidement car je vais bientôt me déconnecter.
-
Aallthekpop dernière édition par
Mais je ne sais pas où vous voulez en venir, les coordonées du milieux A et B sont [5;0,25] ?
-
Mmathtous dernière édition par
Oui, et ce sont justement celles de K. K est donc le milieu de [AB] : c'est plus précis que de dire qu'il est situé à mi-parcours.
Si tu observes ton dernier dessin, tu verras que K est en plus le centre de symétrie pour la figure.
-
Aallthekpop dernière édition par
Ah !...C'était donc aussi subtile que cela? Je vous remerices !
-
Mmathtous dernière édition par
De rien.
A+
-
Mmathtous dernière édition par
Il semble y avoir une erreur de calcul quelque part (à vérifier ...) : la pente maximum est de 0,075 et pas 0,75).
De toute façon, ce n'est pas demandé.
-
Aallthekpop dernière édition par
Bonjour, oui j'ai fait une erreur de frappe lors du dernier message où j'en parlais, car mon calcul initial (si vous remontez un peu plus haut), j'ai bien trouvée cette valeur-ci.
-
Aallthekpop dernière édition par
Je souhaite rajouter une question supplémentaire à ce problème :
Voici la réglementation en vigueur pour l'accès à un E.R.P :
"Lorsqu'une dénivellation ne peut être évitée, un plan incliné de pente inférieure ou égale à 5% doit être aménagé afin de la franchir.
Les valeurs de pentes suivantes sont tolérées exceptionnellement :-jusqu'à 8% sur une longeur inférieure ou égale à 2m;
-jusqu'à 10% sur une longeur inférieur ou égale à 0,50 m.
Un palier de repos est nécessaire en haut et en bas de chaque pla incliné, quelle qu'en soit la longueur. En cas de plan incliné de pente supérieure ou égale à 4%, un palier de repos est nécessaire tous les 10m. (extrait de l'article 2 de l'arrêté du 1er août 2006)On me demande si la rample construite respecte-t-elle les normes d'accès pour personnes handicapées ?
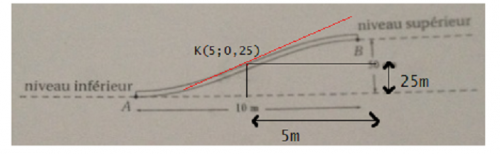
J'ai rajouté nos résultats retrouvés précédemment.Comment calculer le pourcentage des pentes ?
merci encore
-
Mmathtous dernière édition par
Attention : le point K n'est pas situé à 25 m de hauteur, mais à 0,25 m.
La rampe d'accès a une pente maximum de 0,075 soit 7,5% : cela convient donc.
Elle ne fait pas plus de 10 m de long, donc pas besoin de palier de repos (arrivée en haut, la personne est définitivement arrivée) sauf s'il n'y a pas suffisamment de place entre la rampe et la porte.
-
Aallthekpop dernière édition par
Je vous remercies de votre grande aide, vous faites un fantastique travail!
-
Mmathtous dernière édition par
N'exagérons rien.
Bon courage.