Calculer la forme trigonométrique d'un nombre complexe
-
Ssidos dernière édition par Hind
bonjour dans un exo en calculer la forme trigonométrique de z1=√6-i√2/2 en a trouver cosθ\thetaθ=√3/2 et sinθ\thetaθ=-1/2 aprés en a dis que θ\thetaθ1=-pi/6(2pi) j'ai pas compris ca
-
mtschoon dernière édition par

Bonjour,
Si tu n'utilises pas le Latex, mets suffisamment de parenthèses pour que tes formules soient claires.
Je suppose que z1=6−i22z_1=\frac{\sqrt 6-i\sqrt 2}{2}z1=26−i2
Dans ce cas, effectivement
cosθ1=32cos\theta_1=\frac{\sqrt 3}{2}cosθ1=23
sinθ1=−12sin\theta_1=-\frac{1}{2}sinθ1=−21
Pour trouver θ1, utilise les angles remarquables, les angles associés et
fais un schéma pour t'éclairer.Tu dois savoir (angle remarquable) que :
cosπ6=32\cos \frac{\pi}{6}=\frac{\sqrt 3}{2}cos6π=23
sinπ6=12\sin \frac{\pi}{6}=\frac{1}{2}sin6π=21
Or, (angles opposés)
cos(−π6)=cosπ6\cos(- \frac{\pi}{6})=\cos \frac{\pi}{6}cos(−6π)=cos6π
sin(−π6)=−sinπ6\sin( -\frac{\pi}{6})=-\sin \frac{\pi}{6}sin(−6π)=−sin6π
Donc
cos(−π6)=32\cos(- \frac{\pi}{6})=\frac{\sqrt 3}{2}cos(−6π)=23
sin(−π6)=−12\sin( -\frac{\pi}{6})=-\frac{1}{2}sin(−6π)=−21
D'où la réponse.
-
Ssidos dernière édition par
c'est pas plutot contraire cos pi/6=1/2 et sin pi/6=racine3/2
-
mtschoon dernière édition par

Non.
Tu confonds avec ∏/3
Comme je te l'ai déjà dit, fais un schéma pour t'éclairer.
-
Ssidos dernière édition par
j'ai pas compri
-
mtschoon dernière édition par

Je t'avais conseillé de faire un schéma .
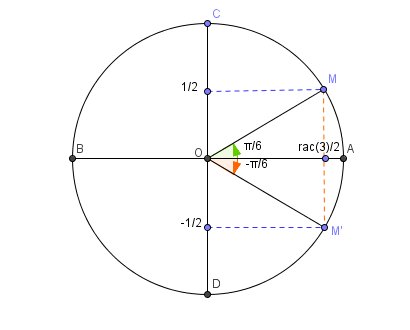
Si tu ne l'as pas fait, en voici un (cercle trigonométrique)
Observe le avec soin
-
Ssidos dernière édition par
c'est bon j'ai compris merci bien
-
mtschoon dernière édition par

De rien !